verify-that-x-and-x-are-the-solution-of-the-homogeneous-equation-corresponding-to-1-x-y-2-xy-1-y-2-x-1-2-x-0-lt-x-lt-1-and-find-the-general-solution-

Tinku Tara June 3, 2023 Differential Equation 0 Comments

Question Number 133403 by Engr_Jidda last updated on 21/Feb/21

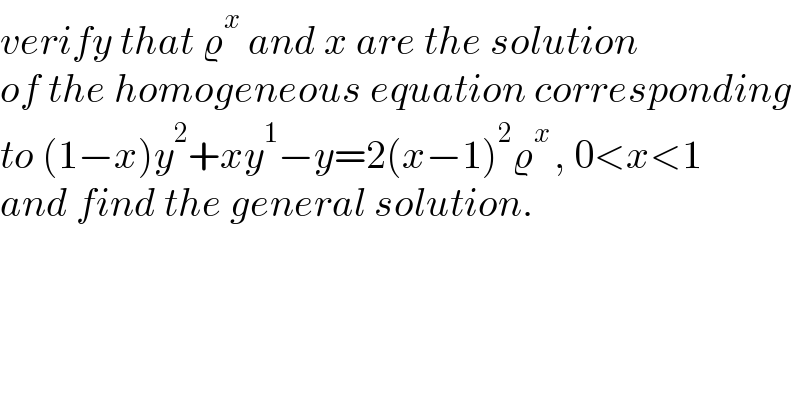
verify that ϱ^x and x are the solution of the homogeneous equation corresponding to (1−x)y^2 +xy^1 −y=2(x−1)^2 ϱ^(x ) , 0<x<1 and find the general solution.

$${verify}\:{that}\:\varrho^{{x}} \:{and}\:{x}\:{are}\:{the}\:{solution} \\ $$$${of}\:{the}\:{homogeneous}\:{equation}\:{corresponding} \\ $$$${to}\:\left(\mathrm{1}−{x}\right){y}^{\mathrm{2}} +{xy}^{\mathrm{1}} −{y}=\mathrm{2}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \varrho^{{x}\:} ,\:\mathrm{0}<{x}<\mathrm{1} \\ $$$${and}\:{find}\:{the}\:{general}\:{solution}. \\ $$

Facebook Tweet Pin

verify-that-x-and-x-are-the-solution-of-the-homogeneous-equation-corresponding-to-1-x-y-2-xy-1-y-2-x-1-2-x-0-lt-x-lt-1-and-find-the-general-solution-

Leave a Reply Cancel reply