Menu Close

W-f-x-t-0-1-t-f-x-ln-xt-dx-t-gt-0-W-f-x-g-x-t-W-f-x-t-W-g-x-t-W-cf-x-t-cW-f-x-t-W-1-t-W-x-t-W-x-n-t-n-N-W-f-x-t-

Tinku Tara 0 Comments
Pin




Question Number 1351 by 123456 last updated on 24/Jul/15
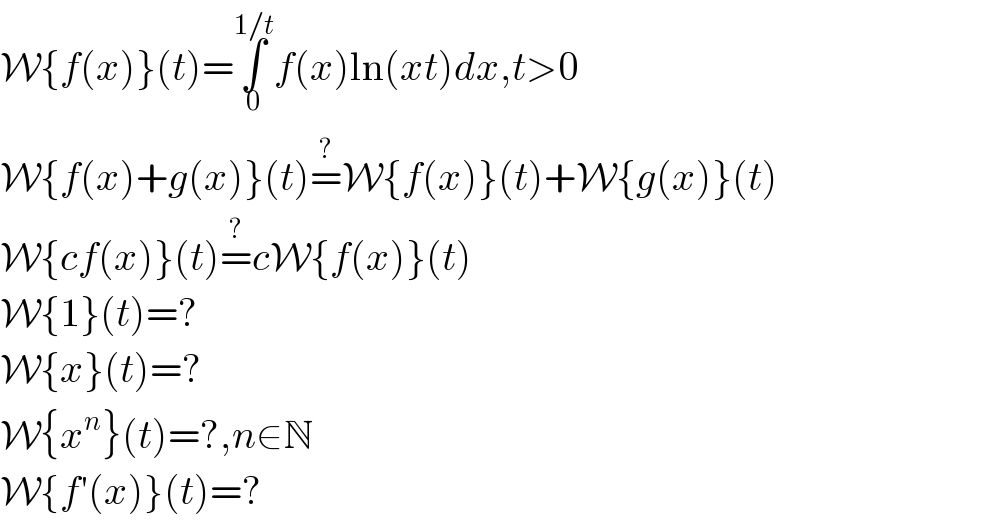
W{f(x)}(t)=∫_0 ^(1/t) f(x)ln(xt)dx,t>0 W{f(x)+g(x)}(t)=^? W{f(x)}(t)+W{g(x)}(t) W{cf(x)}(t)=^? cW{f(x)}(t) W{1}(t)=? W{x}(t)=? W{x^n }(t)=?,n∈N W{f′(x)}(t)=?
$$\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}/{t}} {\int}}{f}\left({x}\right)\mathrm{ln}\left({xt}\right){dx},{t}>\mathrm{0} \\ $$$$\mathcal{W}\left\{{f}\left({x}\right)+{g}\left({x}\right)\right\}\left({t}\right)\overset{?} {=}\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right)+\mathcal{W}\left\{{g}\left({x}\right)\right\}\left({t}\right) \\ $$$$\mathcal{W}\left\{{cf}\left({x}\right)\right\}\left({t}\right)\overset{?} {=}{c}\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right) \\ $$$$\mathcal{W}\left\{\mathrm{1}\right\}\left({t}\right)=? \\ $$$$\mathcal{W}\left\{{x}\right\}\left({t}\right)=? \\ $$$$\mathcal{W}\left\{{x}^{{n}} \right\}\left({t}\right)=?,{n}\in\mathbb{N} \\ $$$$\mathcal{W}\left\{{f}'\left({x}\right)\right\}\left({t}\right)=? \\ $$
Commented by 112358 last updated on 25/Jul/15
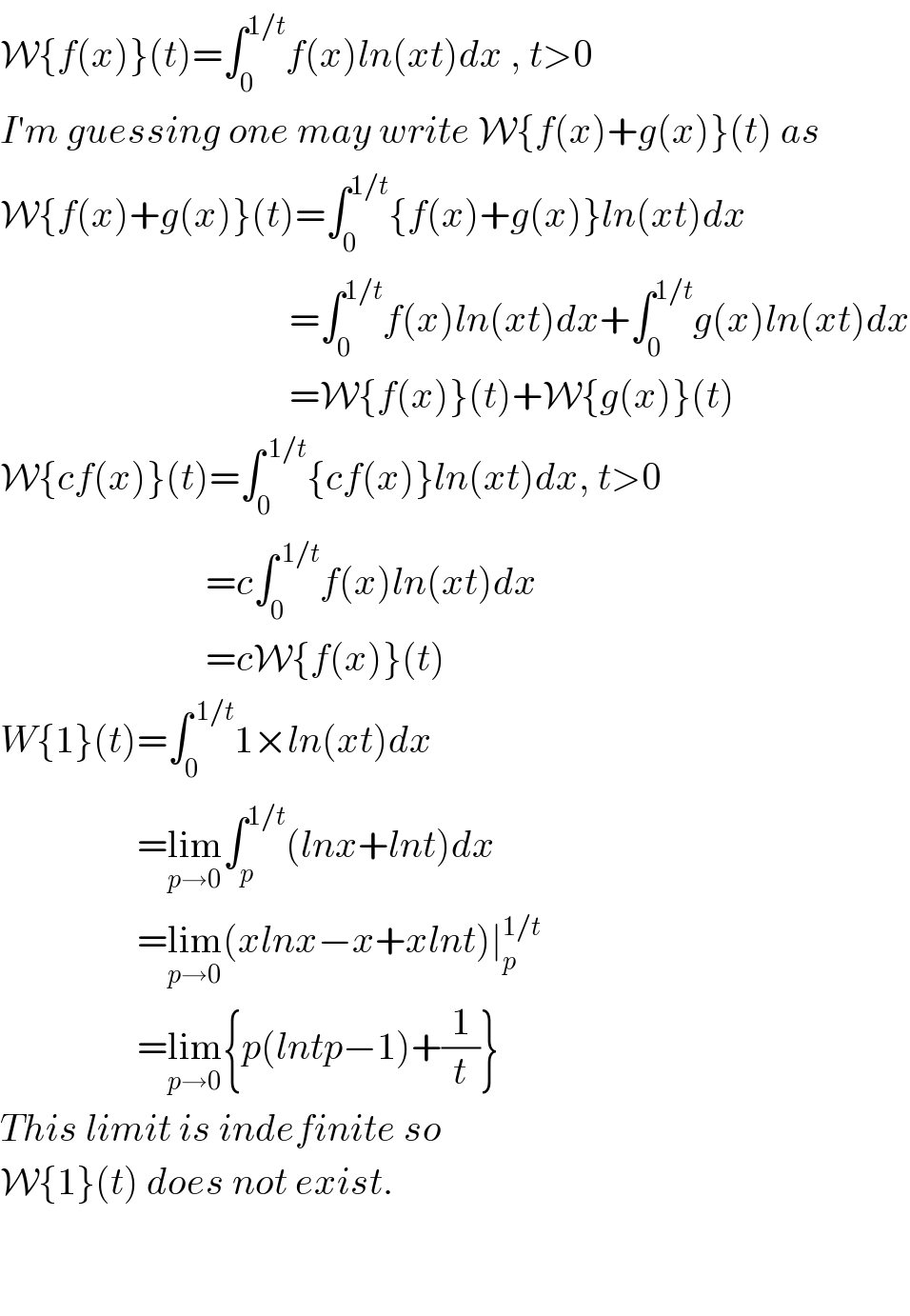
W{f(x)}(t)=∫_0 ^(1/t) f(x)ln(xt)dx , t>0 I′m guessing one may write W{f(x)+g(x)}(t) as W{f(x)+g(x)}(t)=∫_0 ^(1/t) {f(x)+g(x)}ln(xt)dx =∫_0 ^(1/t) f(x)ln(xt)dx+∫_0 ^(1/t) g(x)ln(xt)dx =W{f(x)}(t)+W{g(x)}(t) W{cf(x)}(t)=∫_0 ^( 1/t) {cf(x)}ln(xt)dx, t>0 =c∫_0 ^( 1/t) f(x)ln(xt)dx =cW{f(x)}(t) W{1}(t)=∫_0 ^( 1/t) 1×ln(xt)dx =lim_(p→0) ∫_p ^(1/t) (lnx+lnt)dx =lim_(p→0) (xlnx−x+xlnt)∣_p ^(1/t) =lim_(p→0) {p(lntp−1)+(1/t)} This limit is indefinite so W{1}(t) does not exist.
$$\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{1}/{t}} {f}\left({x}\right){ln}\left({xt}\right){dx}\:,\:{t}>\mathrm{0} \\ $$$${I}'{m}\:{guessing}\:{one}\:{may}\:{write}\:\mathcal{W}\left\{{f}\left({x}\right)+{g}\left({x}\right)\right\}\left({t}\right)\:{as} \\ $$$$\mathcal{W}\left\{{f}\left({x}\right)+{g}\left({x}\right)\right\}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{1}/{t}} \left\{{f}\left({x}\right)+{g}\left({x}\right)\right\}{ln}\left({xt}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}/{t}} {f}\left({x}\right){ln}\left({xt}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}/{t}} {g}\left({x}\right){ln}\left({xt}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right)+\mathcal{W}\left\{{g}\left({x}\right)\right\}\left({t}\right) \\ $$$$\mathcal{W}\left\{{cf}\left({x}\right)\right\}\left({t}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}/{t}} \left\{{cf}\left({x}\right)\right\}{ln}\left({xt}\right){dx},\:{t}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={c}\int_{\mathrm{0}} ^{\:\mathrm{1}/{t}} {f}\left({x}\right){ln}\left({xt}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={c}\mathcal{W}\left\{{f}\left({x}\right)\right\}\left({t}\right) \\ $$$${W}\left\{\mathrm{1}\right\}\left({t}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}/{t}} \mathrm{1}×{ln}\left({xt}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{p}} ^{\mathrm{1}/{t}} \left({lnx}+{lnt}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({xlnx}−{x}+{xlnt}\right)\mid_{{p}} ^{\mathrm{1}/{t}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{{p}\left({lntp}−\mathrm{1}\right)+\frac{\mathrm{1}}{{t}}\right\} \\ $$$${This}\:{limit}\:{is}\:{indefinite}\:{so}\: \\ $$$$\mathcal{W}\left\{\mathrm{1}\right\}\left({t}\right)\:{does}\:{not}\:{exist}. \\ $$$$ \\ $$$$ \\ $$
Commented by 112358 last updated on 25/Jul/15
W{x}(t)=∫_0 ^(1/t) xlnxt dx W{x^n }(t)=∫_0 ^(1/t) x^n lnxt dx W{f^′ (x)}(t)=∫_0 ^(1/t) f^′ (x)lnxt dx =f(x)lnxt∣_0 ^(1/t) −∫_0 ^(1/t) ((f(x))/x)dx These three integrals do no exist.
$$\mathcal{W}\left\{{x}\right\}\left({t}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}/{t}} {\int}}{xlnxt}\:{dx} \\ $$$$\mathcal{W}\left\{{x}^{{n}} \right\}\left({t}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}/{t}} {\int}}{x}^{{n}} {lnxt}\:{dx} \\ $$$$\mathcal{W}\left\{{f}^{'} \left({x}\right)\right\}\left({t}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}/{t}} {\int}}{f}^{'} \left({x}\right){lnxt}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={f}\left({x}\right){lnxt}\mid_{\mathrm{0}} ^{\mathrm{1}/{t}} −\underset{\mathrm{0}} {\overset{\mathrm{1}/{t}} {\int}}\frac{{f}\left({x}\right)}{{x}}{dx} \\ $$$${These}\:{three}\:{integrals}\:{do}\:{no}\:{exist}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *