Question Number 12499 by tawa last updated on 23/Apr/17

$$\mathrm{Water}\:\mathrm{flows}\:\mathrm{out}\:\mathrm{of}\:\mathrm{a}\:\mathrm{tank}\:\mathrm{through}\:\mathrm{a}\:\mathrm{hole}\:\mathrm{of}\:\mathrm{diameter}\:\mathrm{2cm}\:\mathrm{above}\:\mathrm{the}\:\mathrm{hole} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Determine}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{outflow} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{The}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{outflow}\:\mathrm{when}\:\mathrm{the}\:\mathrm{level}\:\mathrm{of}\:\mathrm{the}\:\mathrm{water}\:\mathrm{in}\:\mathrm{the}\:\mathrm{tank}\:\mathrm{is}\:\mathrm{2cm}\:\mathrm{above} \\ $$$$\mathrm{the}\:\mathrm{hole}.\: \\ $$
Answered by sandy_suhendra last updated on 24/Apr/17
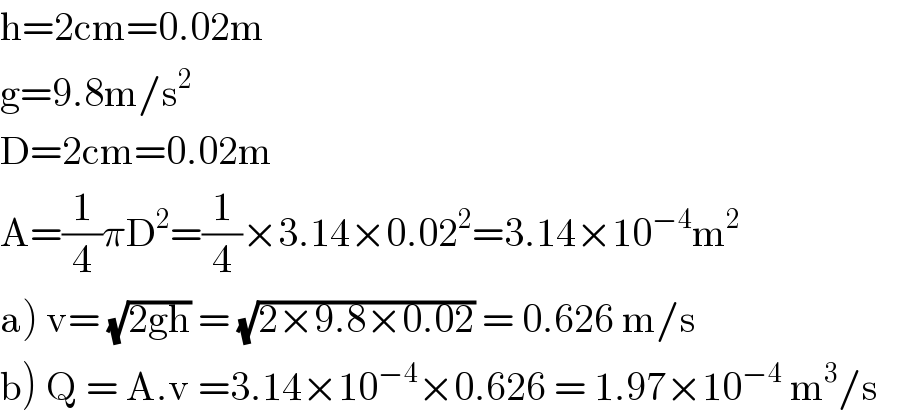
$$\mathrm{h}=\mathrm{2cm}=\mathrm{0}.\mathrm{02m} \\ $$$$\mathrm{g}=\mathrm{9}.\mathrm{8m}/\mathrm{s}^{\mathrm{2}} \\ $$$$\mathrm{D}=\mathrm{2cm}=\mathrm{0}.\mathrm{02m} \\ $$$$\mathrm{A}=\frac{\mathrm{1}}{\mathrm{4}}\pi\mathrm{D}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{3}.\mathrm{14}×\mathrm{0}.\mathrm{02}^{\mathrm{2}} =\mathrm{3}.\mathrm{14}×\mathrm{10}^{−\mathrm{4}} \mathrm{m}^{\mathrm{2}} \:\:\:\:\: \\ $$$$\left.\mathrm{a}\right)\:\mathrm{v}=\:\sqrt{\mathrm{2gh}}\:=\:\sqrt{\mathrm{2}×\mathrm{9}.\mathrm{8}×\mathrm{0}.\mathrm{02}}\:=\:\mathrm{0}.\mathrm{626}\:\mathrm{m}/\mathrm{s}\:\:\:\:\: \\ $$$$\left.\mathrm{b}\right)\:\mathrm{Q}\:=\:\mathrm{A}.\mathrm{v}\:=\mathrm{3}.\mathrm{14}×\mathrm{10}^{−\mathrm{4}} ×\mathrm{0}.\mathrm{626}\:=\:\mathrm{1}.\mathrm{97}×\mathrm{10}^{−\mathrm{4}} \:\mathrm{m}^{\mathrm{3}} /\mathrm{s}\:\:\:\:\: \\ $$
Commented by tawa last updated on 24/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
