Question Number 12566 by JAZAR last updated on 25/Apr/17

$${we}\:{give}\:{U}_{\mathrm{1}} ,{U}_{\mathrm{2}} ,{U}_{\mathrm{3}} \:{the}\:{terms}\:{of}\:{a}\:{geometric}\:{sequence} \\ $$$$.{Determine}\:{U}_{\mathrm{1}} ,{U}_{\mathrm{2}} ,{U}_{\mathrm{3}} \:{such}\:{that}\:: \\ $$$$ \\ $$$$\begin{cases}{{U}_{\mathrm{1}} .{U}_{\mathrm{2}} .{U}_{\mathrm{3}} =\mathrm{64}}\\{{U}_{\mathrm{1}} ^{\mathrm{2}} +{U}_{\mathrm{2}} ^{\mathrm{2}} +{U}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{84}}\end{cases} \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 25/Apr/17
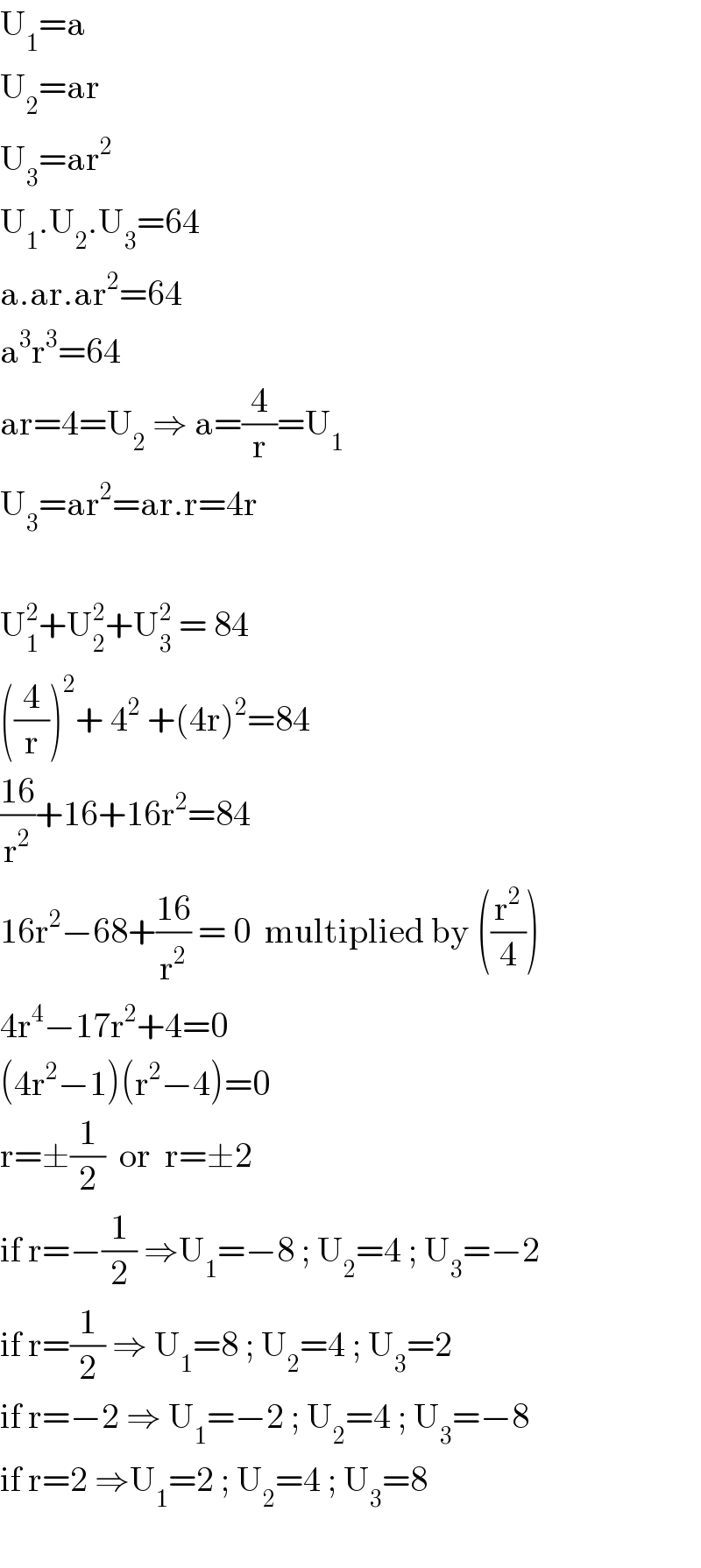
$$\mathrm{U}_{\mathrm{1}} =\mathrm{a} \\ $$$$\mathrm{U}_{\mathrm{2}} =\mathrm{ar} \\ $$$$\mathrm{U}_{\mathrm{3}} =\mathrm{ar}^{\mathrm{2}} \\ $$$$\mathrm{U}_{\mathrm{1}} .\mathrm{U}_{\mathrm{2}} .\mathrm{U}_{\mathrm{3}} =\mathrm{64} \\ $$$$\mathrm{a}.\mathrm{ar}.\mathrm{ar}^{\mathrm{2}} =\mathrm{64} \\ $$$$\mathrm{a}^{\mathrm{3}} \mathrm{r}^{\mathrm{3}} =\mathrm{64} \\ $$$$\mathrm{ar}=\mathrm{4}=\mathrm{U}_{\mathrm{2}} \:\Rightarrow\:\mathrm{a}=\frac{\mathrm{4}}{\mathrm{r}}=\mathrm{U}_{\mathrm{1}} \\ $$$$\mathrm{U}_{\mathrm{3}} =\mathrm{ar}^{\mathrm{2}} =\mathrm{ar}.\mathrm{r}=\mathrm{4r} \\ $$$$ \\ $$$$\mathrm{U}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{U}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{U}_{\mathrm{3}} ^{\mathrm{2}} \:=\:\mathrm{84} \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{r}}\right)^{\mathrm{2}} +\:\mathrm{4}^{\mathrm{2}} \:+\left(\mathrm{4r}\right)^{\mathrm{2}} =\mathrm{84} \\ $$$$\frac{\mathrm{16}}{\mathrm{r}^{\mathrm{2}} }+\mathrm{16}+\mathrm{16r}^{\mathrm{2}} =\mathrm{84} \\ $$$$\mathrm{16r}^{\mathrm{2}} −\mathrm{68}+\frac{\mathrm{16}}{\mathrm{r}^{\mathrm{2}} }\:=\:\mathrm{0}\:\:\mathrm{multiplied}\:\mathrm{by}\:\left(\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{4}}\right)\:\:\:\:\: \\ $$$$\mathrm{4r}^{\mathrm{4}} −\mathrm{17r}^{\mathrm{2}} +\mathrm{4}=\mathrm{0} \\ $$$$\left(\mathrm{4r}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{r}^{\mathrm{2}} −\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{r}=\pm\frac{\mathrm{1}}{\mathrm{2}}\:\:\mathrm{or}\:\:\mathrm{r}=\pm\mathrm{2} \\ $$$$\mathrm{if}\:\mathrm{r}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{U}_{\mathrm{1}} =−\mathrm{8}\:;\:\mathrm{U}_{\mathrm{2}} =\mathrm{4}\:;\:\mathrm{U}_{\mathrm{3}} =−\mathrm{2}\:\:\:\:\: \\ $$$$\mathrm{if}\:\mathrm{r}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\mathrm{U}_{\mathrm{1}} =\mathrm{8}\:;\:\mathrm{U}_{\mathrm{2}} =\mathrm{4}\:;\:\mathrm{U}_{\mathrm{3}} =\mathrm{2} \\ $$$$\mathrm{if}\:\mathrm{r}=−\mathrm{2}\:\Rightarrow\:\mathrm{U}_{\mathrm{1}} =−\mathrm{2}\:;\:\mathrm{U}_{\mathrm{2}} =\mathrm{4}\:;\:\mathrm{U}_{\mathrm{3}} =−\mathrm{8} \\ $$$$\mathrm{if}\:\mathrm{r}=\mathrm{2}\:\Rightarrow\mathrm{U}_{\mathrm{1}} =\mathrm{2}\:;\:\mathrm{U}_{\mathrm{2}} =\mathrm{4}\:;\:\mathrm{U}_{\mathrm{3}} =\mathrm{8} \\ $$$$ \\ $$
