Question Number 5165 by 1771727373 last updated on 24/Apr/16

$${what}\:{is} \\ $$$$\sqrt{{i}+\mathrm{1}}\:\:\:\:? \\ $$
Commented by FilupSmith last updated on 24/Apr/16
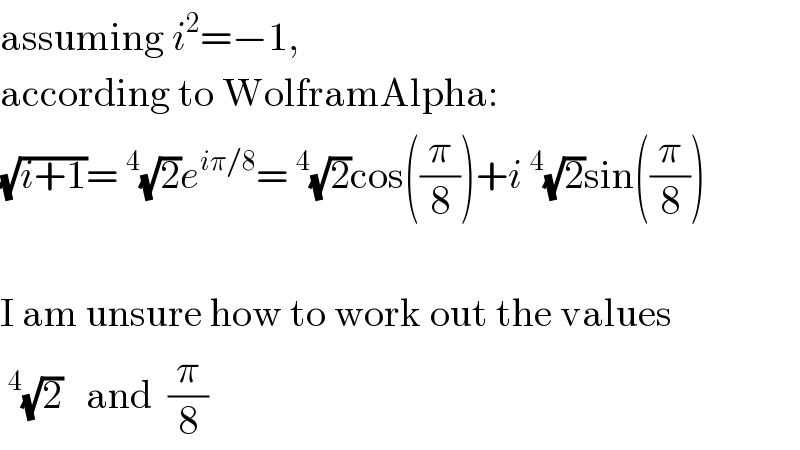
$$\mathrm{assuming}\:{i}^{\mathrm{2}} =−\mathrm{1}, \\ $$$$\mathrm{according}\:\mathrm{to}\:\mathrm{WolframAlpha}: \\ $$$$\sqrt{{i}+\mathrm{1}}=\:^{\mathrm{4}} \sqrt{\mathrm{2}}{e}^{{i}\pi/\mathrm{8}} =\:^{\mathrm{4}} \sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{8}}\right)+{i}\:^{\mathrm{4}} \sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{8}}\right) \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{work}\:\mathrm{out}\:\mathrm{the}\:\mathrm{values} \\ $$$$\:^{\mathrm{4}} \sqrt{\mathrm{2}}\:\:\:\mathrm{and}\:\:\frac{\pi}{\mathrm{8}} \\ $$
Answered by 123456 last updated on 24/Apr/16
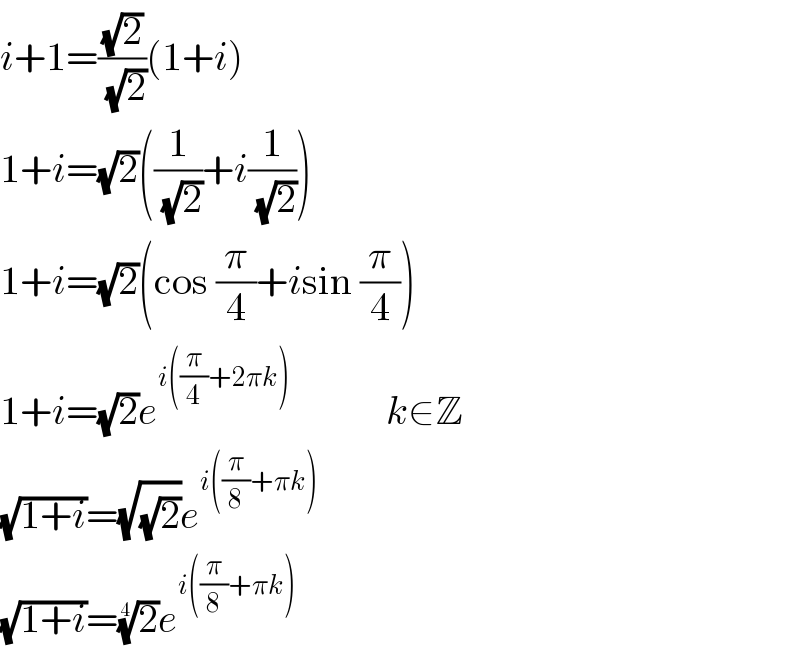
$${i}+\mathrm{1}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{1}+{i}\right) \\ $$$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+{i}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+{i}\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}{e}^{{i}\left(\frac{\pi}{\mathrm{4}}+\mathrm{2}\pi{k}\right)} \:\:\:\:\:\:\:\:\:\:\:\:{k}\in\mathbb{Z} \\ $$$$\sqrt{\mathrm{1}+{i}}=\sqrt{\sqrt{\mathrm{2}}}{e}^{{i}\left(\frac{\pi}{\mathrm{8}}+\pi{k}\right)} \\ $$$$\sqrt{\mathrm{1}+{i}}=\sqrt[{\mathrm{4}}]{\mathrm{2}}{e}^{{i}\left(\frac{\pi}{\mathrm{8}}+\pi{k}\right)} \\ $$
