Question Number 132382 by liberty last updated on 13/Feb/21
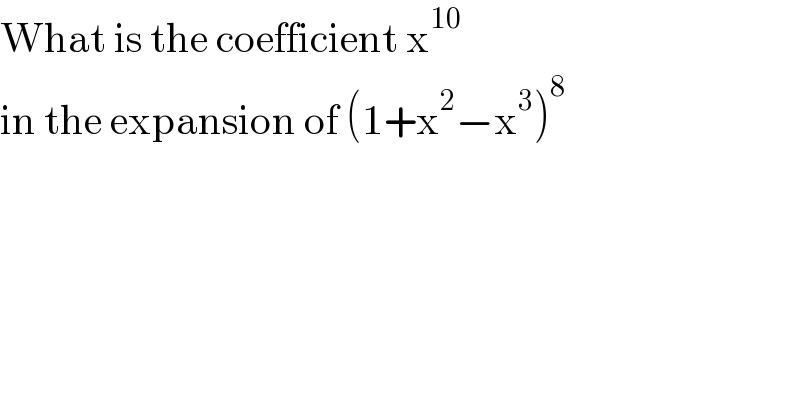
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{x}^{\mathrm{10}} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{8}} \\ $$
Answered by EDWIN88 last updated on 13/Feb/21

$$\mathrm{by}\:\mathrm{multinomial}\:\mathrm{theorem}\:;\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{10}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{from}\:\mathrm{2}\:\mathrm{cases} \\ $$$$\left(\mathrm{1}\right)\left(\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{5}} \left(−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{0}} \:\mathrm{with}\:\mathrm{coefficient}\:\begin{pmatrix}{\:\:\:\:\mathrm{8}}\\{\mathrm{3},\mathrm{5},\mathrm{0}}\end{pmatrix} \\ $$$$=\:\frac{\mathrm{8}!}{\mathrm{3}!.\mathrm{5}!.\mathrm{0}!}\:=\:\frac{\mathrm{8}.\mathrm{7}.\mathrm{6}}{\mathrm{6}}=\mathrm{56} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} \:\mathrm{with}\:\mathrm{coefficient}\:\begin{pmatrix}{\:\:\:\:\mathrm{8}}\\{\mathrm{4},\mathrm{2},\mathrm{2}}\end{pmatrix} \\ $$$$=\:\frac{\mathrm{8}!}{\mathrm{4}!.\mathrm{2}!.\mathrm{2}!}\:=\:\frac{\mathrm{8}.\mathrm{7}.\mathrm{6}.\mathrm{5}}{\mathrm{4}}=\:\mathrm{420} \\ $$$$\mathrm{totally}\:=\:\mathrm{476} \\ $$
