Question Number 66285 by Rio Michael last updated on 12/Aug/19
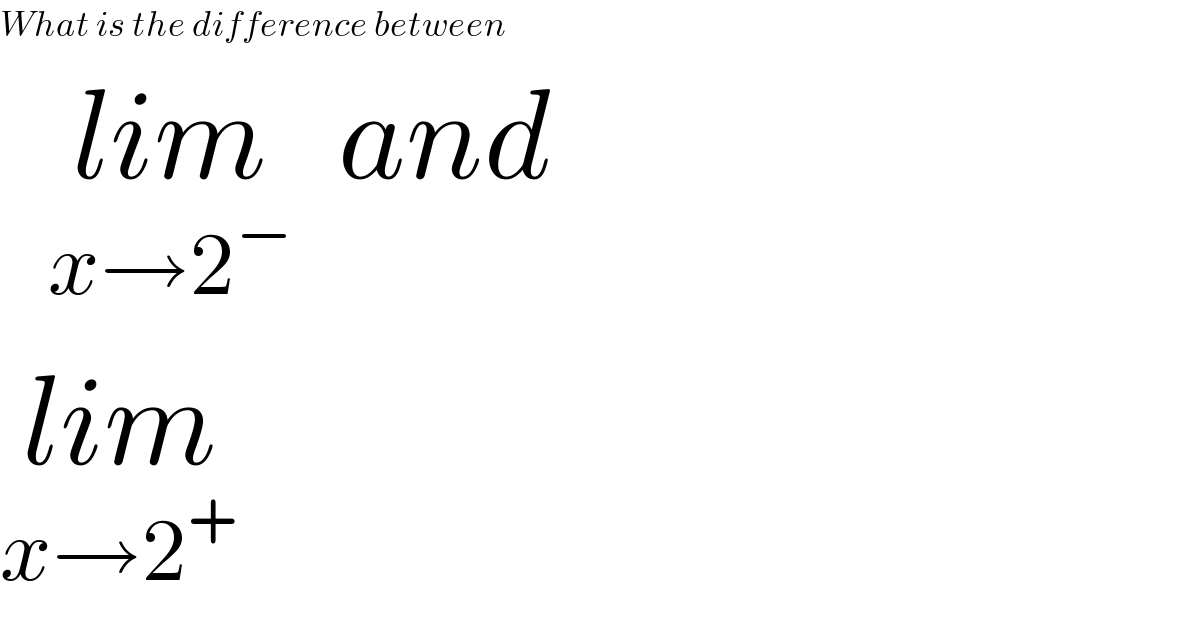
$${What}\:{is}\:{the}\:{difference}\:{between} \\ $$$$\:\:\underset{{x}\rightarrow\mathrm{2}^{−} } {{lim}}\:\:{and} \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{+} } {{lim}} \\ $$
Answered by MJS last updated on 12/Aug/19

$$\mathrm{limit}\:\mathrm{from}\:\mathrm{left}\:\mathrm{respectively}\:\mathrm{right}\:\mathrm{side}.\:\mathrm{the} \\ $$$$\mathrm{two}\:\mathrm{limits}\:\mathrm{can}\:\mathrm{be}\:\mathrm{different} \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}−\mathrm{2}}\:=−\infty \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}−\mathrm{2}}=+\infty \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\sqrt[{{x}}]{{x}^{\mathrm{2}} }\:=+\infty \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\sqrt[{{x}}]{{x}^{\mathrm{2}} }\:=\mathrm{0} \\ $$
Answered by GordonYeeman last updated on 12/Aug/19

$${the}\:{limit}\:{x}\rightarrow\mathrm{2}\:{consists}\:{on}\:{taking}\: \\ $$$${arbitrarily}\:{close}\:{values}\:{of}\:\mathrm{2}\:\left(\mathrm{1}.\mathrm{99},\right. \\ $$$$\left.\mathrm{1}.\mathrm{9999},\mathrm{1}.\mathrm{999999}…\right).\:{x}\rightarrow\mathrm{2}^{+} \:{is}\:{basically} \\ $$$${the}\:{same}\:{but}\:{those}\:{values}\:{must}\:{be}\: \\ $$$${greater}\:{than}\:\mathrm{2}\:\left(\mathrm{2}.\mathrm{01},\:\mathrm{2}.\mathrm{000001},\:{etc}\right).\: \\ $$$${In}\:{the}\:{case}\:{of}\:{x}\rightarrow\mathrm{2}^{−} \:{they}\:{must}\:{be} \\ $$$${smaller} \\ $$
Commented by Rio Michael last updated on 12/Aug/19

$${thank}\:{you}\:{sirs} \\ $$
