Question Number 135695 by liberty last updated on 15/Mar/21
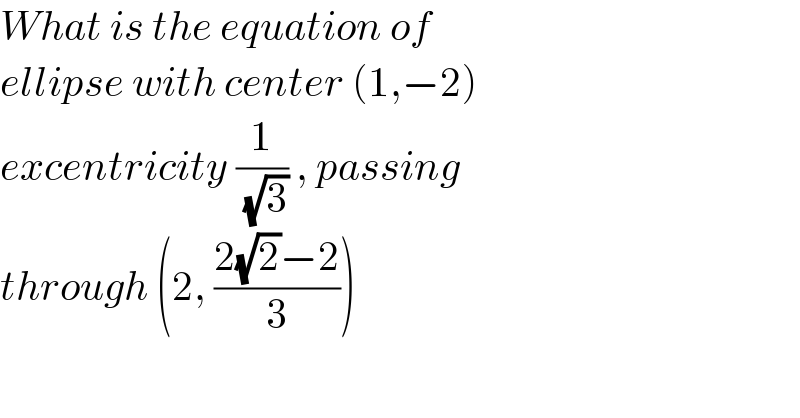
$${What}\:{is}\:{the}\:{equation}\:{of} \\ $$$${ellipse}\:{with}\:{center}\:\left(\mathrm{1},−\mathrm{2}\right)\: \\ $$$${excentricity}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:,\:{passing} \\ $$$${through}\:\left(\mathrm{2},\:\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{3}}\right)\: \\ $$
Answered by mr W last updated on 15/Mar/21
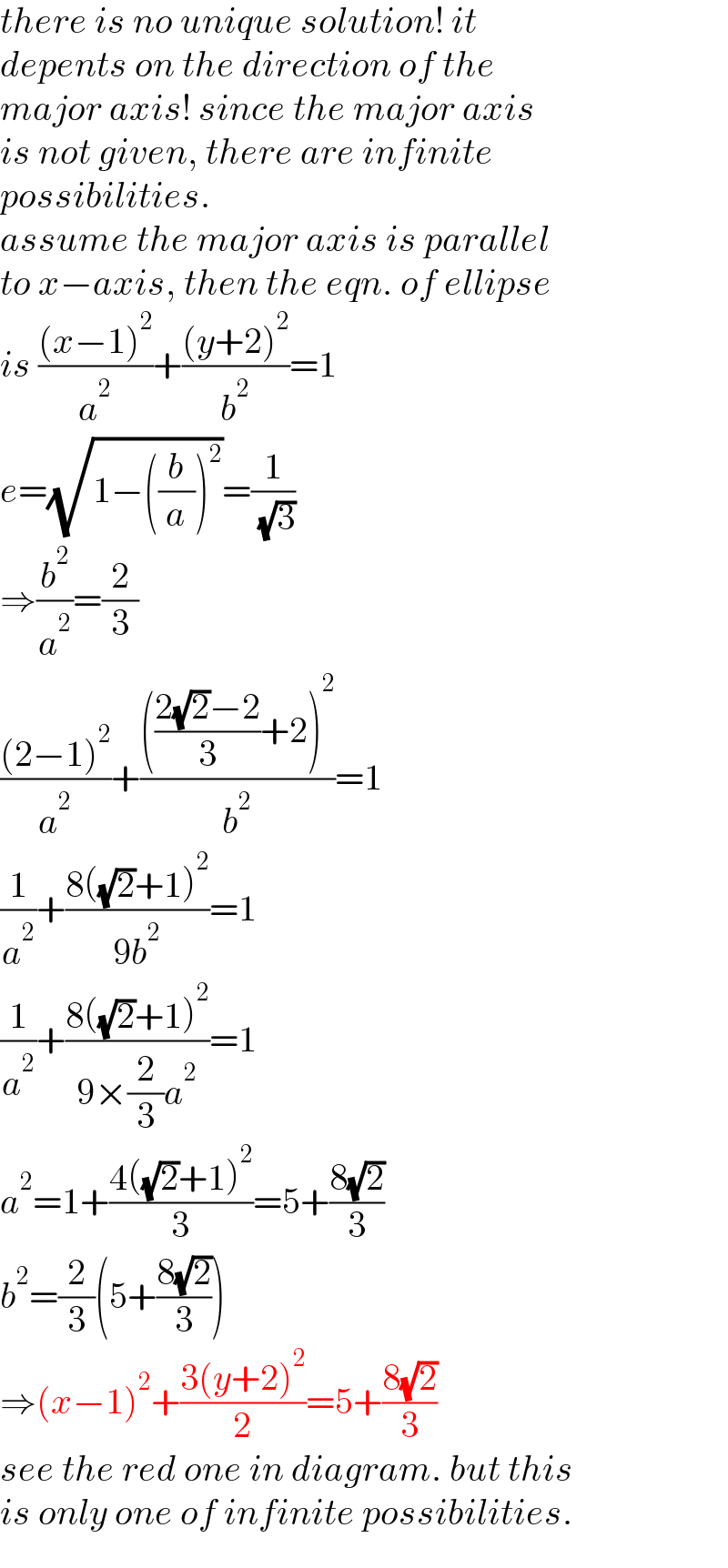
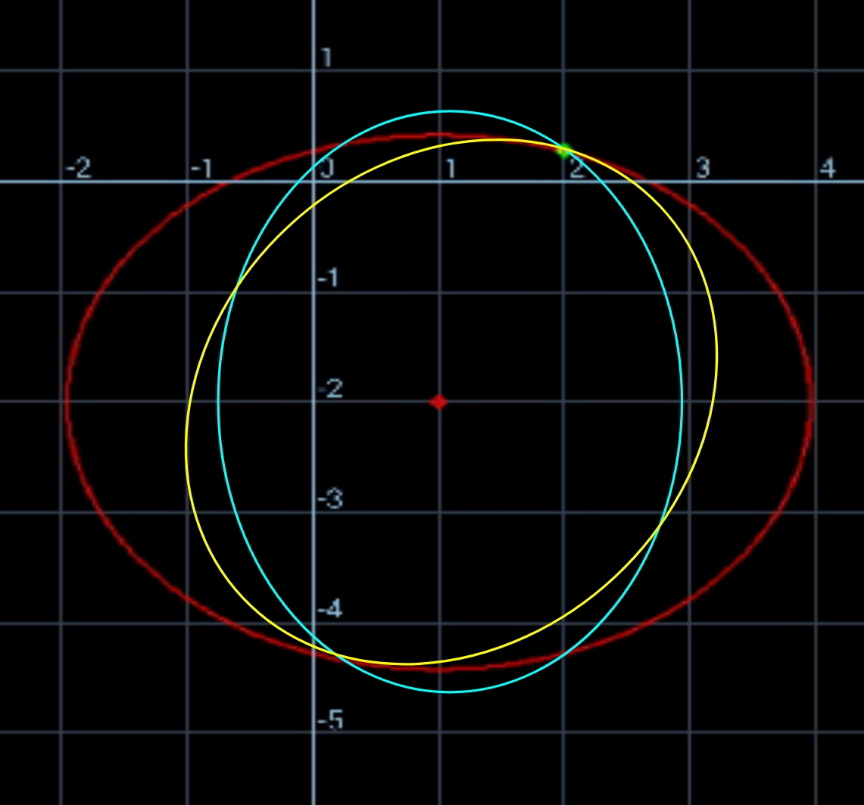
$${there}\:{is}\:{no}\:{unique}\:{solution}!\:{it}\: \\ $$$${depents}\:{on}\:{the}\:{direction}\:{of}\:{the} \\ $$$${major}\:{axis}!\:{since}\:{the}\:{major}\:{axis} \\ $$$${is}\:{not}\:{given},\:{there}\:{are}\:{infinite} \\ $$$${possibilities}. \\ $$$${assume}\:{the}\:{major}\:{axis}\:{is}\:{parallel} \\ $$$${to}\:{x}−{axis},\:{then}\:{the}\:{eqn}.\:{of}\:{ellipse} \\ $$$${is}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}+\mathrm{2}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${e}=\sqrt{\mathrm{1}−\left(\frac{{b}}{{a}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{\left(\mathrm{2}−\mathrm{1}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{3}}+\mathrm{2}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{8}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{8}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}×\frac{\mathrm{2}}{\mathrm{3}}{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$${a}^{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{4}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}}=\mathrm{5}+\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{5}+\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{3}\left({y}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{5}+\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${see}\:{the}\:{red}\:{one}\:{in}\:{diagram}.\:{but}\:{this} \\ $$$${is}\:{only}\:{one}\:{of}\:{infinite}\:{possibilities}. \\ $$
Commented by mr W last updated on 15/Mar/21
Commented by liberty last updated on 15/Mar/21

$${agree}\:{sir} \\ $$
