Question Number 75392 by wo1lxjwjdb last updated on 10/Dec/19
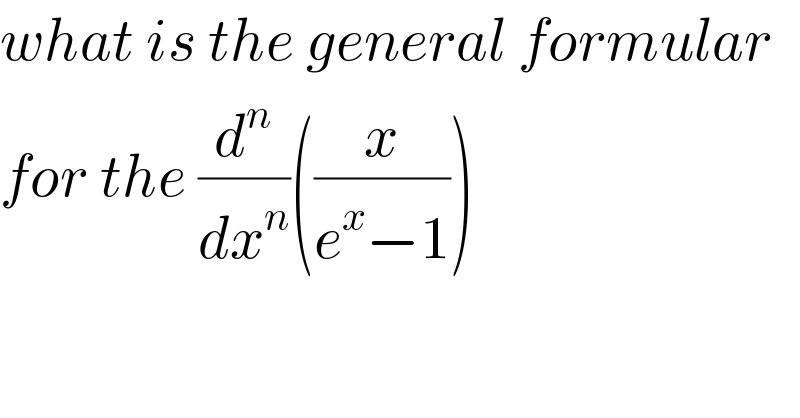
$${what}\:{is}\:{the}\:{general}\:{formular} \\ $$$${for}\:{the}\:\frac{{d}^{{n}} }{{dx}^{{n}} }\left(\frac{{x}}{{e}^{{x}} −\mathrm{1}}\right) \\ $$
Answered by mind is power last updated on 10/Dec/19
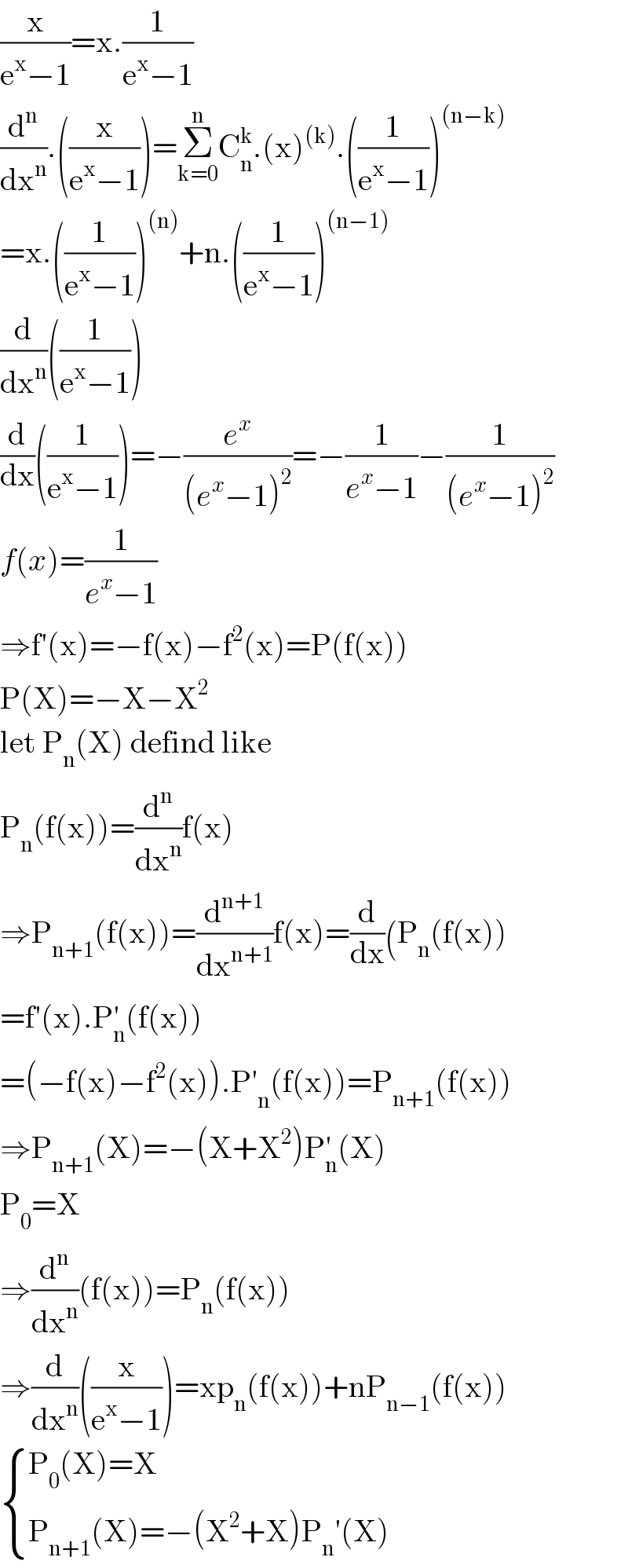
$$\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}=\mathrm{x}.\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}} \\ $$$$\frac{\mathrm{d}^{\mathrm{n}} }{\mathrm{dx}^{\mathrm{n}} }.\left(\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} .\left(\mathrm{x}\right)^{\left(\mathrm{k}\right)} .\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)^{\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$=\mathrm{x}.\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)^{\left(\mathrm{n}\right)} +\mathrm{n}.\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)^{\left(\mathrm{n}−\mathrm{1}\right)} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}^{\mathrm{n}} }\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right) \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)=−\frac{{e}^{{x}} }{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{{e}^{{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{e}^{{x}} −\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)=−\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{P}\left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\mathrm{P}\left(\mathrm{X}\right)=−\mathrm{X}−\mathrm{X}^{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{P}_{\mathrm{n}} \left(\mathrm{X}\right)\:\mathrm{defind}\:\mathrm{like} \\ $$$$\mathrm{P}_{\mathrm{n}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)=\frac{\mathrm{d}^{\mathrm{n}} }{\mathrm{dx}^{\mathrm{n}} }\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{P}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)=\frac{\mathrm{d}^{\mathrm{n}+\mathrm{1}} }{\mathrm{dx}^{\mathrm{n}+\mathrm{1}} }\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{P}_{\mathrm{n}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)\right. \\ $$$$=\mathrm{f}'\left(\mathrm{x}\right).\mathrm{P}_{\mathrm{n}} ^{'} \left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$=\left(−\mathrm{f}\left(\mathrm{x}\right)−\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\right).\mathrm{P}'_{\mathrm{n}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{P}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\Rightarrow\mathrm{P}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{X}\right)=−\left(\mathrm{X}+\mathrm{X}^{\mathrm{2}} \right)\mathrm{P}_{\mathrm{n}} ^{'} \left(\mathrm{X}\right) \\ $$$$\mathrm{P}_{\mathrm{0}} =\mathrm{X} \\ $$$$\Rightarrow\frac{\mathrm{d}^{\mathrm{n}} }{\mathrm{dx}^{\mathrm{n}} }\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{P}_{\mathrm{n}} \left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\Rightarrow\frac{\mathrm{d}}{\mathrm{dx}^{\mathrm{n}} }\left(\frac{\mathrm{x}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)=\mathrm{xp}_{\mathrm{n}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)+\mathrm{nP}_{\mathrm{n}−\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\begin{cases}{\mathrm{P}_{\mathrm{0}} \left(\mathrm{X}\right)=\mathrm{X}}\\{\mathrm{P}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{X}\right)=−\left(\mathrm{X}^{\mathrm{2}} +\mathrm{X}\right)\mathrm{P}_{\mathrm{n}} '\left(\mathrm{X}\right)}\end{cases} \\ $$
