Menu Close

What-is-the-remainder-13-163-when-divided-by-99-

Tinku Tara 0 Comments
Pin




Question Number 137383 by bramlexs22 last updated on 02/Apr/21
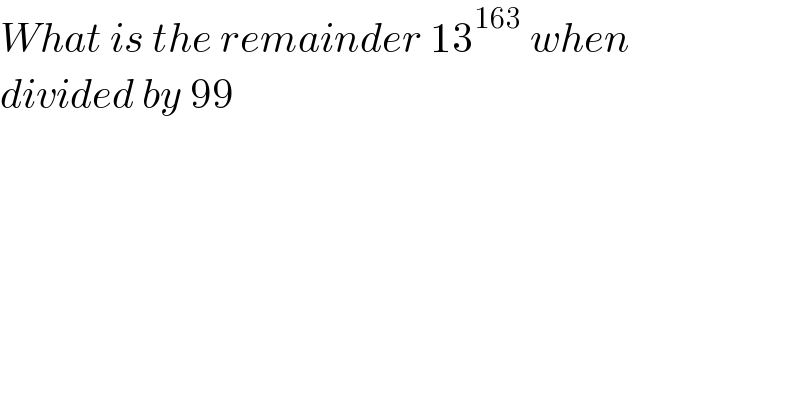
What is the remainder 13^(163) when divided by 99
$${What}\:{is}\:{the}\:{remainder}\:\mathrm{13}^{\mathrm{163}} \:{when} \\ $$$${divided}\:{by}\:\mathrm{99}\: \\ $$
Answered by EDWIN88 last updated on 02/Apr/21
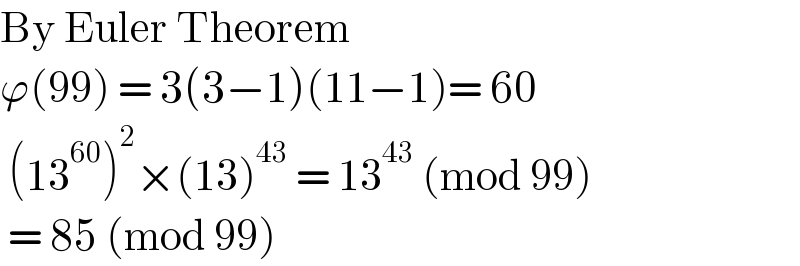
By Euler Theorem ϕ(99) = 3(3−1)(11−1)= 60 (13^(60) )^2 ×(13)^(43) = 13^(43) (mod 99) = 85 (mod 99)
$$\mathrm{By}\:\mathrm{Euler}\:\mathrm{Theorem}\: \\ $$$$\varphi\left(\mathrm{99}\right)\:=\:\mathrm{3}\left(\mathrm{3}−\mathrm{1}\right)\left(\mathrm{11}−\mathrm{1}\right)=\:\mathrm{60}\: \\ $$$$\:\left(\mathrm{13}^{\mathrm{60}} \right)^{\mathrm{2}} ×\left(\mathrm{13}\right)^{\mathrm{43}} \:=\:\mathrm{13}^{\mathrm{43}} \:\left(\mathrm{mod}\:\mathrm{99}\right) \\ $$$$\:=\:\mathrm{85}\:\left(\mathrm{mod}\:\mathrm{99}\right)\: \\ $$
Answered by physicstutes last updated on 02/Apr/21
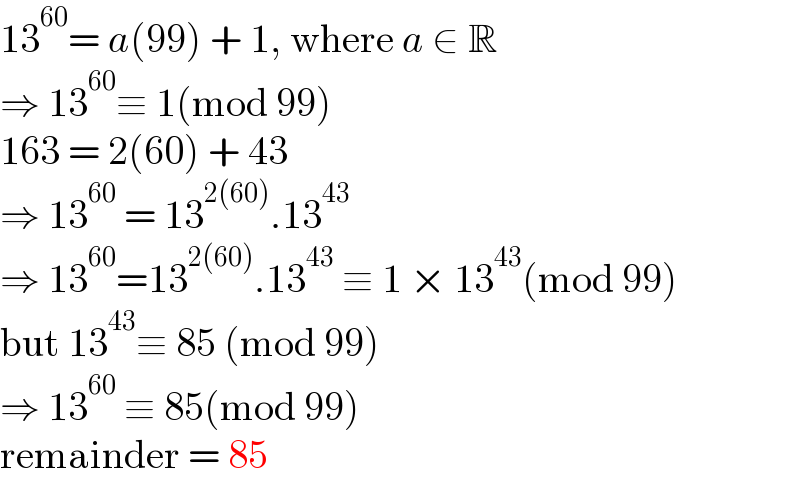
13^(60) = a(99) + 1, where a ∈ R ⇒ 13^(60) ≡ 1(mod 99) 163 = 2(60) + 43 ⇒ 13^(60) = 13^(2(60)) .13^(43) ⇒ 13^(60) =13^(2(60)) .13^(43) ≡ 1 × 13^(43) (mod 99) but 13^(43) ≡ 85 (mod 99) ⇒ 13^(60) ≡ 85(mod 99) remainder = 85
$$\mathrm{13}^{\mathrm{60}} =\:{a}\left(\mathrm{99}\right)\:+\:\mathrm{1},\:\mathrm{where}\:{a}\:\in\:\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{13}^{\mathrm{60}} \equiv\:\mathrm{1}\left(\mathrm{mod}\:\mathrm{99}\right) \\ $$$$\mathrm{163}\:=\:\mathrm{2}\left(\mathrm{60}\right)\:+\:\mathrm{43} \\ $$$$\Rightarrow\:\mathrm{13}^{\mathrm{60}} \:=\:\mathrm{13}^{\mathrm{2}\left(\mathrm{60}\right)} .\mathrm{13}^{\mathrm{43}} \\ $$$$\Rightarrow\:\mathrm{13}^{\mathrm{60}} =\mathrm{13}^{\mathrm{2}\left(\mathrm{60}\right)} .\mathrm{13}^{\mathrm{43}} \:\equiv\:\mathrm{1}\:×\:\mathrm{13}^{\mathrm{43}} \left(\mathrm{mod}\:\mathrm{99}\right) \\ $$$$\mathrm{but}\:\mathrm{13}^{\mathrm{43}} \equiv\:\mathrm{85}\:\left(\mathrm{mod}\:\mathrm{99}\right) \\ $$$$\Rightarrow\:\mathrm{13}^{\mathrm{60}} \:\equiv\:\mathrm{85}\left(\mathrm{mod}\:\mathrm{99}\right) \\ $$$$\mathrm{remainder}\:=\:\mathrm{85} \\ $$
Answered by Rasheed.Sindhi last updated on 02/Apr/21
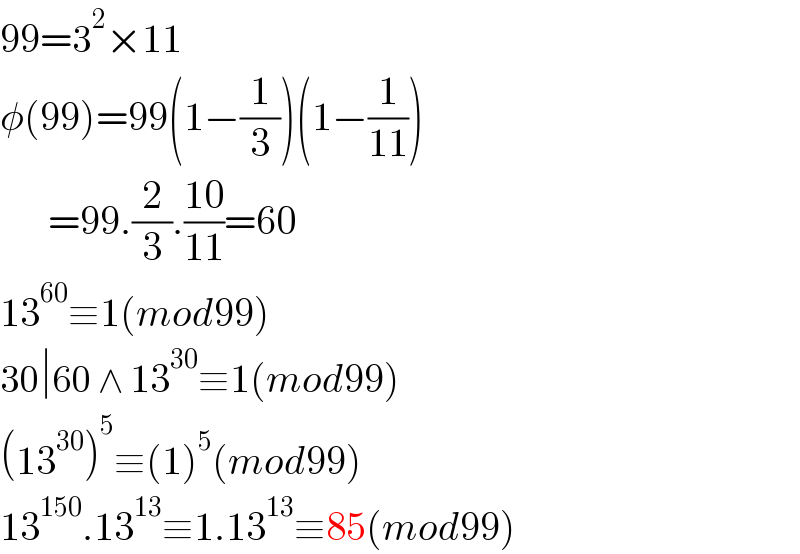
99=3^2 ×11 φ(99)=99(1−(1/3))(1−(1/(11))) =99.(2/3).((10)/(11))=60 13^(60) ≡1(mod99) 30∣60 ∧ 13^(30) ≡1(mod99) (13^(30) )^5 ≡(1)^5 (mod99) 13^(150) .13^(13) ≡1.13^(13) ≡85(mod99)
$$\mathrm{99}=\mathrm{3}^{\mathrm{2}} ×\mathrm{11} \\ $$$$\phi\left(\mathrm{99}\right)=\mathrm{99}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{11}}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{99}.\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{10}}{\mathrm{11}}=\mathrm{60} \\ $$$$\mathrm{13}^{\mathrm{60}} \equiv\mathrm{1}\left({mod}\mathrm{99}\right) \\ $$$$\mathrm{30}\mid\mathrm{60}\:\wedge\:\mathrm{13}^{\mathrm{30}} \equiv\mathrm{1}\left({mod}\mathrm{99}\right) \\ $$$$\left(\mathrm{13}^{\mathrm{30}} \right)^{\mathrm{5}} \equiv\left(\mathrm{1}\right)^{\mathrm{5}} \left({mod}\mathrm{99}\right) \\ $$$$\mathrm{13}^{\mathrm{150}} .\mathrm{13}^{\mathrm{13}} \equiv\mathrm{1}.\mathrm{13}^{\mathrm{13}} \equiv\mathrm{85}\left({mod}\mathrm{99}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *