Question Number 9021 by tawakalitu last updated on 14/Nov/16
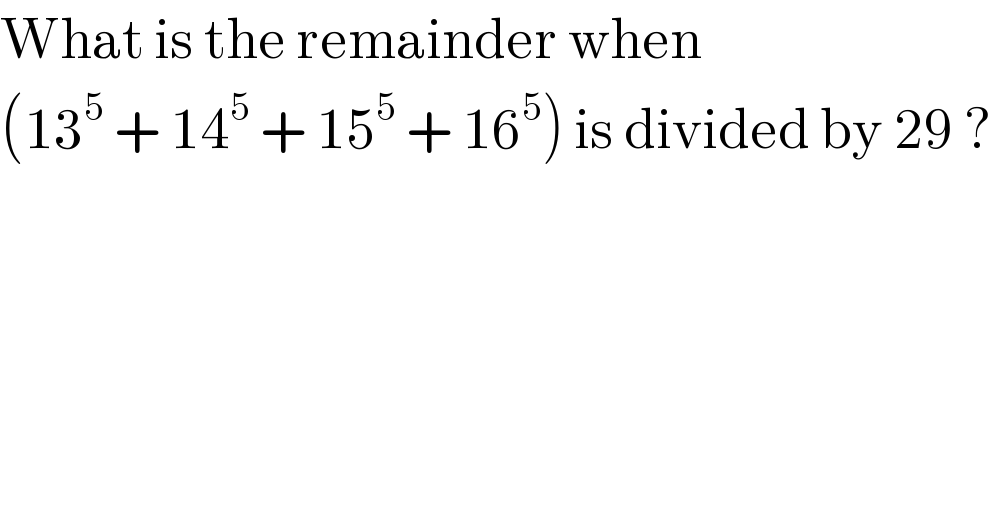
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\: \\ $$$$\left(\mathrm{13}^{\mathrm{5}} \:+\:\mathrm{14}^{\mathrm{5}} \:+\:\mathrm{15}^{\mathrm{5}} \:+\:\mathrm{16}^{\mathrm{5}} \right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{29}\:?\: \\ $$
Answered by aydnmustafa1976 last updated on 14/Nov/16
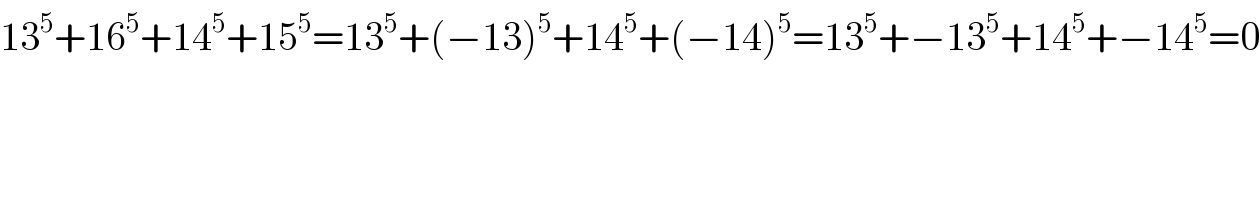
$$\mathrm{13}^{\mathrm{5}} +\mathrm{16}^{\mathrm{5}} +\mathrm{14}^{\mathrm{5}} +\mathrm{15}^{\mathrm{5}} =\mathrm{13}^{\mathrm{5}} +\left(−\mathrm{13}\right)^{\mathrm{5}} +\mathrm{14}^{\mathrm{5}} +\left(−\mathrm{14}\right)^{\mathrm{5}} =\mathrm{13}^{\mathrm{5}} +−\mathrm{13}^{\mathrm{5}} +\mathrm{14}^{\mathrm{5}} +−\mathrm{14}^{\mathrm{5}} =\mathrm{0} \\ $$
Commented by tawakalitu last updated on 14/Nov/16

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
