Menu Close

What-is-the-remainder-when-17-23-is-divided-by-16-

Tinku Tara
Pin




Question Number 95 by rajabhay last updated on 25/Jan/15
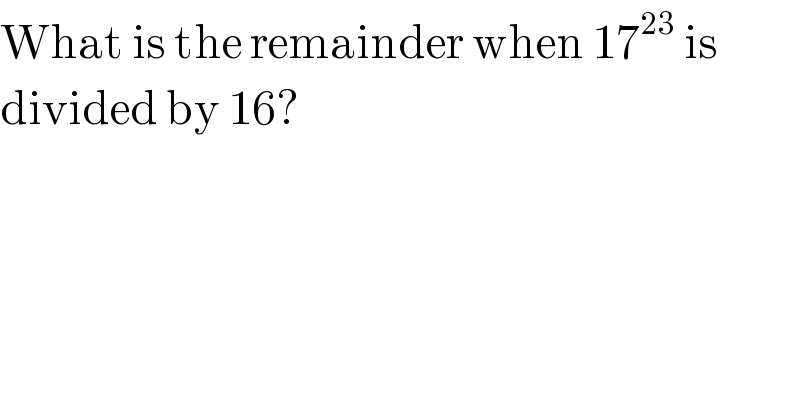
What is the remainder when 17^(23) is divided by 16?
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:\mathrm{17}^{\mathrm{23}} \:\mathrm{is} \\ $$$$\mathrm{divided}\:\mathrm{by}\:\mathrm{16}? \\ $$
Answered by rajabhay last updated on 03/Dec/14
17^(23) =(16+1)^(23) From binomial theorem (a+b)^n =Σ_(k=0) ^n ^n C_k a^k b^(n−k) (16+1)^(23) =^(23) C_0 16^0 1^(23) +^(23) C_1 16^1 1^(22) +...+^(23) C_(23) 16^(23) All terms other than 1st include power of 16. hence remainder=1
$$\mathrm{17}^{\mathrm{23}} =\left(\mathrm{16}+\mathrm{1}\right)^{\mathrm{23}} \\ $$$$\mathrm{From}\:\mathrm{binomial}\:\mathrm{theorem}\: \\ $$$$\left({a}+{b}\right)^{\mathrm{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\:^{{n}} {C}_{{k}} {a}^{{k}} {b}^{{n}−{k}} \\ $$$$\left(\mathrm{16}+\mathrm{1}\right)^{\mathrm{23}} =\:^{\mathrm{23}} {C}_{\mathrm{0}} \mathrm{16}^{\mathrm{0}} \mathrm{1}^{\mathrm{23}} +\:^{\mathrm{23}} {C}_{\mathrm{1}} \mathrm{16}^{\mathrm{1}} \mathrm{1}^{\mathrm{22}} +…+\:^{\mathrm{23}} {C}_{\mathrm{23}} \mathrm{16}^{\mathrm{23}} \\ $$$$\mathrm{All}\:\mathrm{terms}\:\mathrm{other}\:\mathrm{than}\:\mathrm{1st}\:\mathrm{include}\:\mathrm{power}\:\mathrm{of}\:\mathrm{16}. \\ $$$$\mathrm{hence}\:\mathrm{remainder}=\mathrm{1} \\ $$
Answered by 123456 last updated on 22/Dec/14
17^(23) ≡1^(23) ≡1(mod 16)
$$\mathrm{17}^{\mathrm{23}} \equiv\mathrm{1}^{\mathrm{23}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{16}\right) \\ $$

Pin