Question Number 6772 by Tawakalitu. last updated on 24/Jul/16

$${What}\:{is}\:{the}\:{smallest}\:{even}\:{number}\:{greater}\:{than}\:\mathrm{3}\:{that}\:{cannot} \\ $$$${be}\:{expressed}\:{as}\:{the}\:{sum}\:{of}\:{two}\:{prime}\:{numbers}\:? \\ $$
Commented by Yozzii last updated on 24/Jul/16
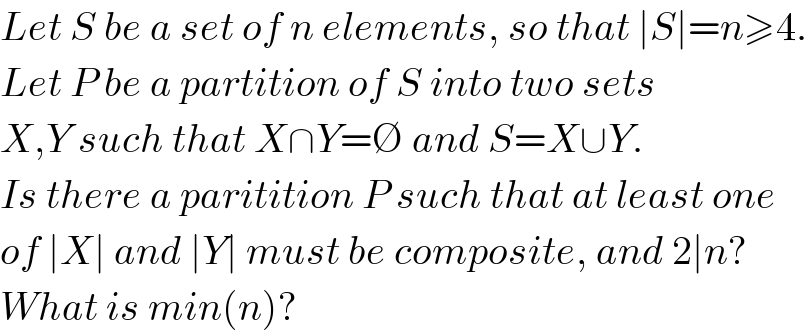
$${Let}\:{S}\:{be}\:{a}\:{set}\:{of}\:{n}\:{elements},\:{so}\:{that}\:\mid{S}\mid={n}\geqslant\mathrm{4}. \\ $$$${Let}\:{P}\:{be}\:{a}\:{partition}\:{of}\:{S}\:{into}\:{two}\:{sets} \\ $$$${X},{Y}\:{such}\:{that}\:{X}\cap{Y}=\varnothing\:{and}\:{S}={X}\cup{Y}. \\ $$$${Is}\:{there}\:{a}\:{paritition}\:{P}\:{such}\:{that}\:{at}\:{least}\:{one} \\ $$$${of}\:\mid{X}\mid\:{and}\:\mid{Y}\mid\:{must}\:{be}\:{composite},\:{and}\:\mathrm{2}\mid{n}?\: \\ $$$${What}\:{is}\:{min}\left({n}\right)? \\ $$
Commented by Tawakalitu. last updated on 24/Jul/16
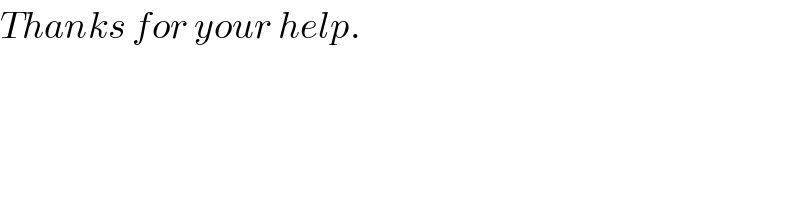
$${Thanks}\:{for}\:{your}\:{help}. \\ $$
Commented by prakash jain last updated on 25/Jul/16
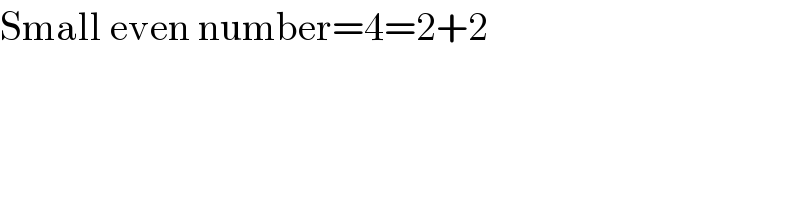
$$\mathrm{Small}\:\mathrm{even}\:\mathrm{number}=\mathrm{4}=\mathrm{2}+\mathrm{2} \\ $$
