Question Number 136607 by EDWIN88 last updated on 23/Mar/21
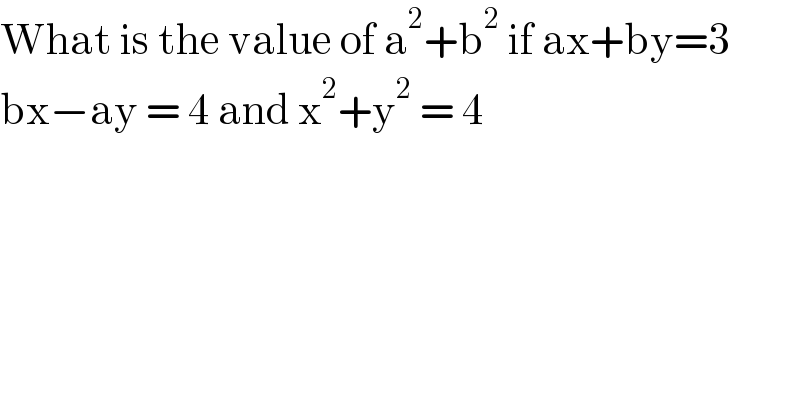
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \:\mathrm{if}\:\mathrm{ax}+\mathrm{by}=\mathrm{3} \\ $$$$\mathrm{bx}−\mathrm{ay}\:=\:\mathrm{4}\:\mathrm{and}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$
Answered by MJS_new last updated on 24/Mar/21
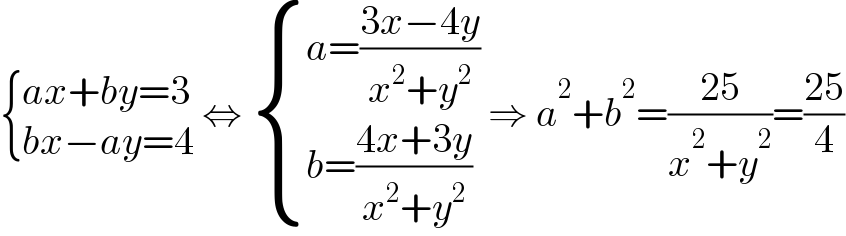
$$\begin{cases}{{ax}+{by}=\mathrm{3}}\\{{bx}−{ay}=\mathrm{4}}\end{cases}\:\Leftrightarrow\:\begin{cases}{{a}=\frac{\mathrm{3}{x}−\mathrm{4}{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\\{{b}=\frac{\mathrm{4}{x}+\mathrm{3}{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\end{cases}\:\Rightarrow\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{25}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\frac{\mathrm{25}}{\mathrm{4}} \\ $$
Answered by mindispower last updated on 24/Mar/21
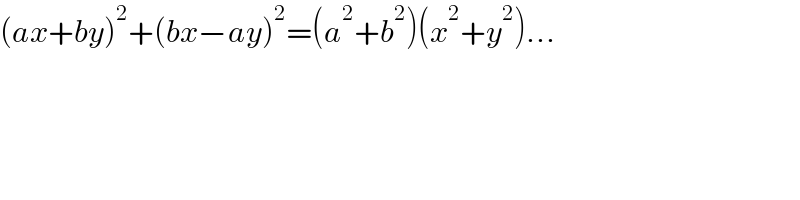
$$\left({ax}+{by}\right)^{\mathrm{2}} +\left({bx}−{ay}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)… \\ $$$$ \\ $$
