what-minimum-value-of-y-sin-x-cosec-x-2-

Question Number 78395 by john santu last updated on 17/Jan/20

w h a t m i n i m u m v a l u e o f

y = \sin x + cosec x + 2

Commented by jagoll last updated on 17/Jan/20

l e t \sin x = t

y = t + \frac{1}{t} + 2

\frac{d y}{d t} = 1 - \frac{1}{t^{2}} = 0 \Rightarrow \frac{(t - 1) (t + 1)}{t^{2}} = 0

\frac{d^{2} y}{{d t}^{2}} = \frac{2}{t^{3}} > 0 f o r t = 1

m i n i m u m i s y = 1 + 1 + 2 = 4

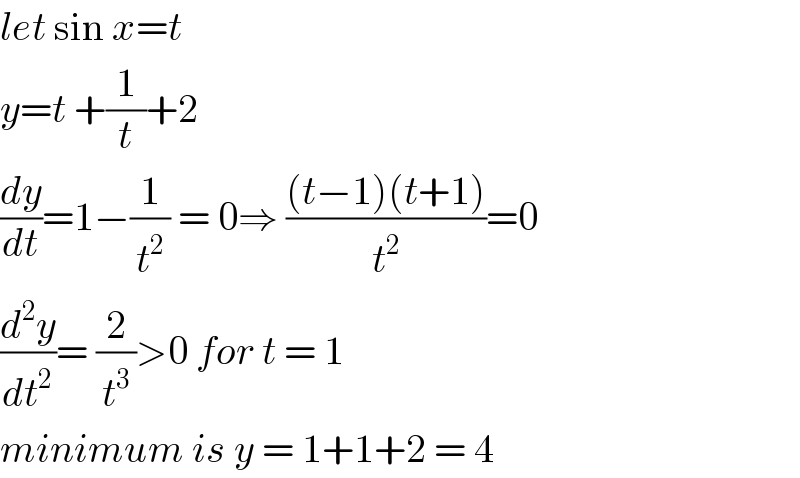
Commented by mr W last updated on 17/Jan/20

n o m a x i m u m a n d n o m i n i m u m s i r!

e x a m p l e :

x \to 0^{+} : y \to + \infty

x \to 0^{-} : y \to - \infty

i n f a c t : y \in [4, + \infty) \land (- \infty, 0]

Commented by john santu last updated on 17/Jan/20

s i r, i f r a n g e o f f u n c t i o n

4 ⩽ y < \infty \land - \infty < y ⩽ 0 t h e n t h e

m i n i m u m v a l u e i s 4 ?

Commented by john santu last updated on 17/Jan/20

m i n i m u m v a l u e a t x = \frac{π}{2} ?

Commented by mr W last updated on 17/Jan/20

n o!

i n t h i s c a s e t h e f u n c t i o n h a s a l o c a l

m i n i m u m 4 a n d a l o c a l m a x i m u m 0 .

w h a t w e g e t f r o m \frac{d y}{d x} = 0 i s a t f i r s t

o n l y a l o c a l m i n i m u m o r a l o c a l

m a x i m u m .

Commented by john santu last updated on 17/Jan/20

o o o k s i r . t h a n k s