Question Number 6832 by Tawakalitu. last updated on 30/Jul/16
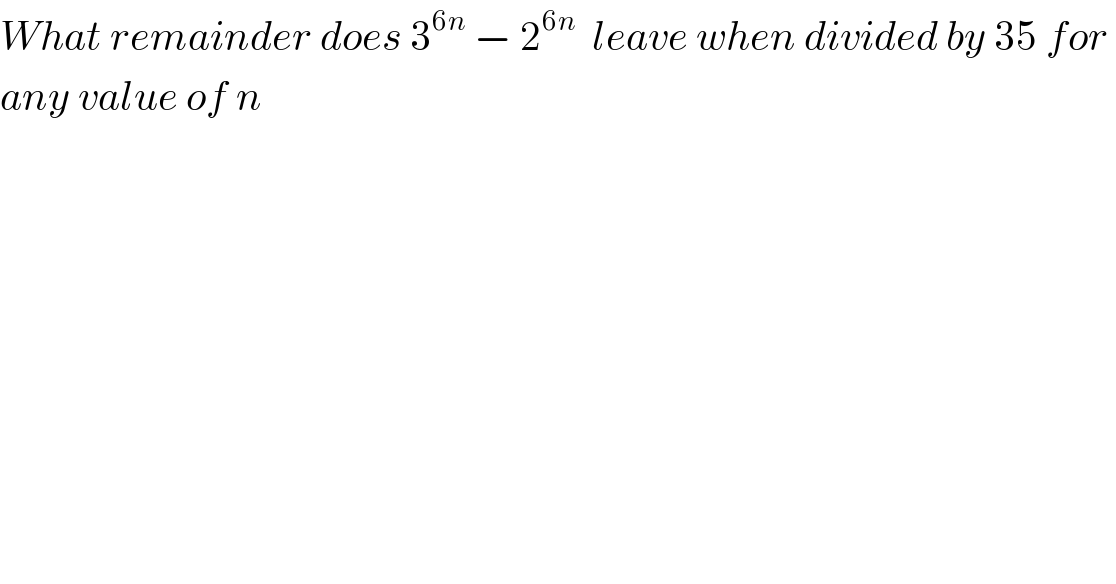
$${What}\:{remainder}\:{does}\:\mathrm{3}^{\mathrm{6}{n}} \:−\:\mathrm{2}^{\mathrm{6}{n}} \:\:{leave}\:{when}\:{divided}\:{by}\:\mathrm{35}\:{for}\: \\ $$$${any}\:{value}\:{of}\:{n}\: \\ $$
Commented by Yozzii last updated on 30/Jul/16
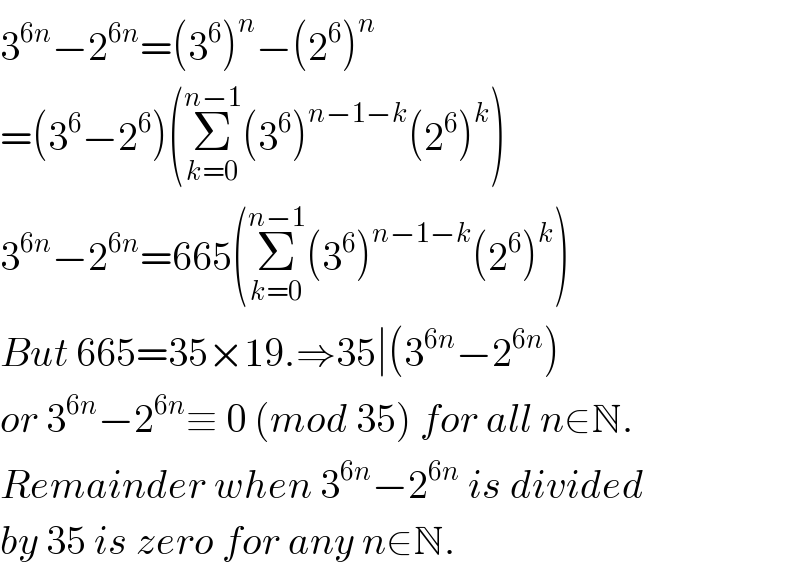
$$\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} =\left(\mathrm{3}^{\mathrm{6}} \right)^{{n}} −\left(\mathrm{2}^{\mathrm{6}} \right)^{{n}} \\ $$$$=\left(\mathrm{3}^{\mathrm{6}} −\mathrm{2}^{\mathrm{6}} \right)\left(\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\mathrm{3}^{\mathrm{6}} \right)^{{n}−\mathrm{1}−{k}} \left(\mathrm{2}^{\mathrm{6}} \right)^{{k}} \right) \\ $$$$\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} =\mathrm{665}\left(\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left(\mathrm{3}^{\mathrm{6}} \right)^{{n}−\mathrm{1}−{k}} \left(\mathrm{2}^{\mathrm{6}} \right)^{{k}} \right) \\ $$$${But}\:\mathrm{665}=\mathrm{35}×\mathrm{19}.\Rightarrow\mathrm{35}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right) \\ $$$${or}\:\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \equiv\:\mathrm{0}\:\left({mod}\:\mathrm{35}\right)\:{for}\:{all}\:{n}\in\mathbb{N}. \\ $$$${Remainder}\:{when}\:\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \:{is}\:{divided} \\ $$$${by}\:\mathrm{35}\:{is}\:{zero}\:{for}\:{any}\:{n}\in\mathbb{N}. \\ $$
Commented by nburiburu last updated on 30/Jul/16
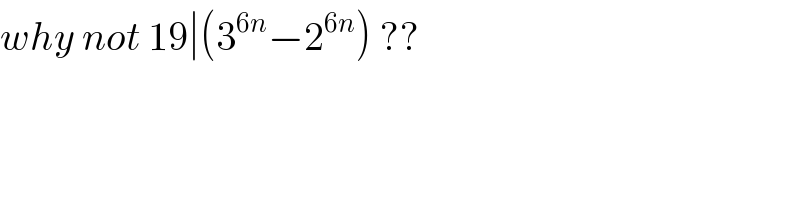
$${why}\:{not}\:\mathrm{19}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right)\:?? \\ $$
Commented by Yozzii last updated on 30/Jul/16
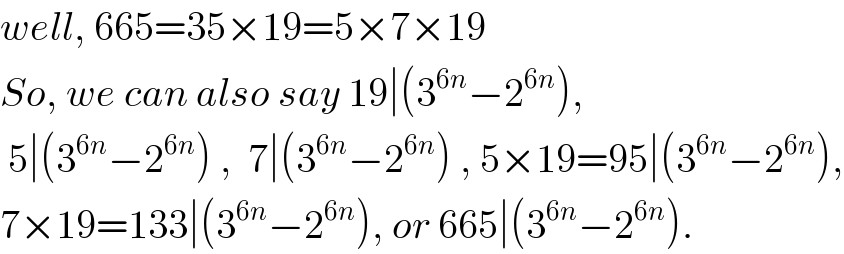
$${well},\:\mathrm{665}=\mathrm{35}×\mathrm{19}=\mathrm{5}×\mathrm{7}×\mathrm{19} \\ $$$${So},\:{we}\:{can}\:{also}\:{say}\:\mathrm{19}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right), \\ $$$$\:\mathrm{5}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right)\:,\:\:\mathrm{7}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right)\:,\:\mathrm{5}×\mathrm{19}=\mathrm{95}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right), \\ $$$$\mathrm{7}×\mathrm{19}=\mathrm{133}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right),\:{or}\:\mathrm{665}\mid\left(\mathrm{3}^{\mathrm{6}{n}} −\mathrm{2}^{\mathrm{6}{n}} \right). \\ $$
Commented by Tawakalitu. last updated on 30/Jul/16

$${Thanks}\:{so}\:{much} \\ $$
