Question Number 5121 by Yozzii last updated on 15/Apr/16
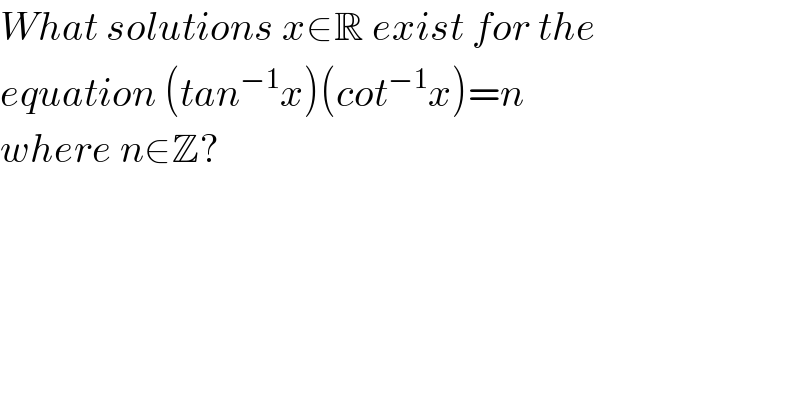
$${What}\:{solutions}\:{x}\in\mathbb{R}\:{exist}\:{for}\:{the}\: \\ $$$${equation}\:\left({tan}^{−\mathrm{1}} {x}\right)\left({cot}^{−\mathrm{1}} {x}\right)={n} \\ $$$${where}\:{n}\in\mathbb{Z}? \\ $$
Answered by prakash jain last updated on 16/Apr/16
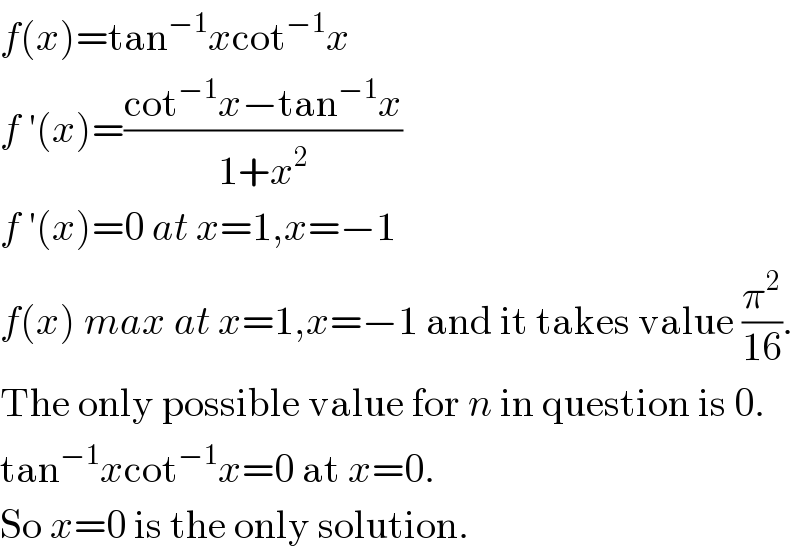
$${f}\left({x}\right)=\mathrm{tan}^{−\mathrm{1}} {x}\mathrm{cot}^{−\mathrm{1}} {x} \\ $$$${f}\:'\left({x}\right)=\frac{\mathrm{cot}^{−\mathrm{1}} {x}−\mathrm{tan}^{−\mathrm{1}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${f}\:'\left({x}\right)=\mathrm{0}\:{at}\:{x}=\mathrm{1},{x}=−\mathrm{1} \\ $$$${f}\left({x}\right)\:{max}\:{at}\:{x}=\mathrm{1},{x}=−\mathrm{1}\:\mathrm{and}\:\mathrm{it}\:\mathrm{takes}\:\mathrm{value}\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}. \\ $$$$\mathrm{The}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{for}\:{n}\:\mathrm{in}\:\mathrm{question}\:\mathrm{is}\:\mathrm{0}. \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}\mathrm{cot}^{−\mathrm{1}} {x}=\mathrm{0}\:\mathrm{at}\:{x}=\mathrm{0}. \\ $$$$\mathrm{So}\:{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}. \\ $$
