Question Number 133053 by pete last updated on 18/Feb/21

$$\mathrm{When}\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{f}\left({x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{4}\:\mathrm{and}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is}\:\mathrm{divided} \\ $$$$\left(\mathrm{x}−\mathrm{3}\right)\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{7}.\:\mathrm{Given}\:\mathrm{that}\:\mathrm{f}\left({x}\right) \\ $$$$\mathrm{may}\:\mathrm{be}\:\mathrm{written}\:\mathrm{in}\:\mathrm{the}\:\mathrm{formf}\left({x}\right)=\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)\mathrm{Q}\left(\mathrm{x}\right)+\mathrm{ax}+\mathrm{b}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{divided} \\ $$$$\mathrm{by}\:\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right).\:\mathrm{If}\:\mathrm{also}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{cubic}\:\mathrm{function} \\ $$$$\mathrm{in}\:\mathrm{which}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{unity}\:\mathrm{and} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1},\:\mathrm{determine}\:\mathrm{Q}\left(\mathrm{x}\right). \\ $$
Answered by EDWIN88 last updated on 18/Feb/21
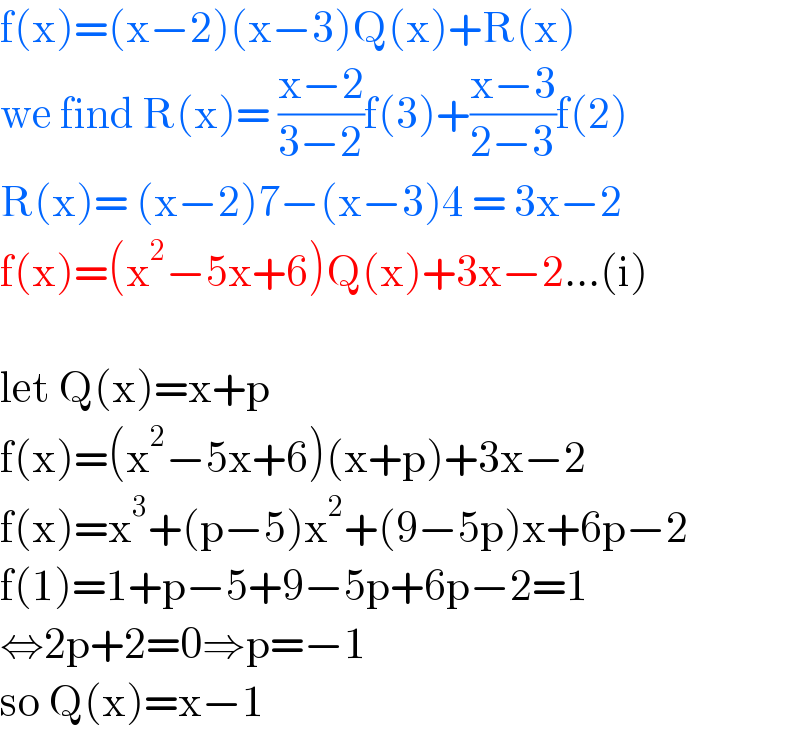
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)\mathrm{Q}\left(\mathrm{x}\right)+\mathrm{R}\left(\mathrm{x}\right) \\ $$$$\mathrm{we}\:\mathrm{find}\:\mathrm{R}\left(\mathrm{x}\right)=\:\frac{\mathrm{x}−\mathrm{2}}{\mathrm{3}−\mathrm{2}}\mathrm{f}\left(\mathrm{3}\right)+\frac{\mathrm{x}−\mathrm{3}}{\mathrm{2}−\mathrm{3}}\mathrm{f}\left(\mathrm{2}\right) \\ $$$$\mathrm{R}\left(\mathrm{x}\right)=\:\left(\mathrm{x}−\mathrm{2}\right)\mathrm{7}−\left(\mathrm{x}−\mathrm{3}\right)\mathrm{4}\:=\:\mathrm{3x}−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}\right)\mathrm{Q}\left(\mathrm{x}\right)+\mathrm{3x}−\mathrm{2}…\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}+\mathrm{p} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}\right)\left(\mathrm{x}+\mathrm{p}\right)+\mathrm{3x}−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{3}} +\left(\mathrm{p}−\mathrm{5}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{9}−\mathrm{5p}\right)\mathrm{x}+\mathrm{6p}−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{p}−\mathrm{5}+\mathrm{9}−\mathrm{5p}+\mathrm{6p}−\mathrm{2}=\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{2p}+\mathrm{2}=\mathrm{0}\Rightarrow\mathrm{p}=−\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}−\mathrm{1} \\ $$
Commented by pete last updated on 18/Feb/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
