When-the-price-of-egg-was-raised-by-2-an-egg-the-number-of-eggs-which-can-be-bought-for-120-is-reduced-by-5-What-is-the-present-price-of-the-egg-

Question Number 6792 by Tawakalitu. last updated on 26/Jul/16

You can't use 'macro parameter character #' in math mode

You can't use 'macro parameter character #' in math mode

p r e s e n t p r i c e o f t h e e g g .

Commented by Yozzii last updated on 27/Jul/16

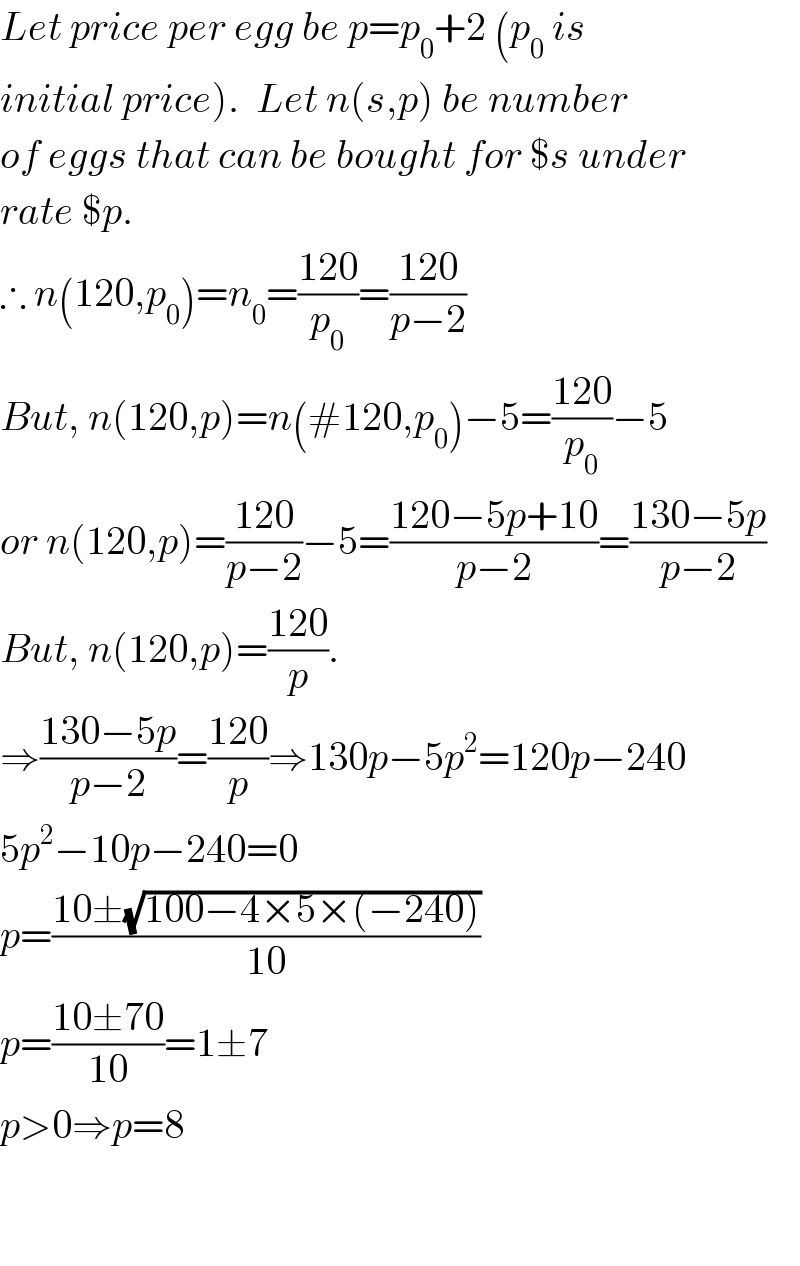
L e t p r i c e p e r e g g b e p = p_{0} + 2 (p_{0} i s

i n i t i a l p r i c e) . L e t n (s, p) b e n u m b e r

o f e g g s t h a t c a n b e b o u g h t f o r $ s u n d e r

r a t e $ p .

∴ n (120, p_{0}) = n_{0} = \frac{120}{p_{0}} = \frac{120}{p - 2}

You can't use 'macro parameter character #' in math mode

o r n (120, p) = \frac{120}{p - 2} - 5 = \frac{120 - 5 p + 10}{p - 2} = \frac{130 - 5 p}{p - 2}

B u t, n (120, p) = \frac{120}{p} .

\Rightarrow \frac{130 - 5 p}{p - 2} = \frac{120}{p} \Rightarrow 130 p - 5 p^{2} = 120 p - 240

5 p^{2} - 10 p - 240 = 0

p = \frac{10 \pm \sqrt{100 - 4 \times 5 \times (- 240)}}{10}

p = \frac{10 \pm 70}{10} = 1 \pm 7

p > 0 \Rightarrow p = 8

Commented by Tawakalitu. last updated on 27/Jul/16

T h a n k s s o m u c h f o r y o u r h e l p