Question Number 5158 by 1771727373 last updated on 24/Apr/16
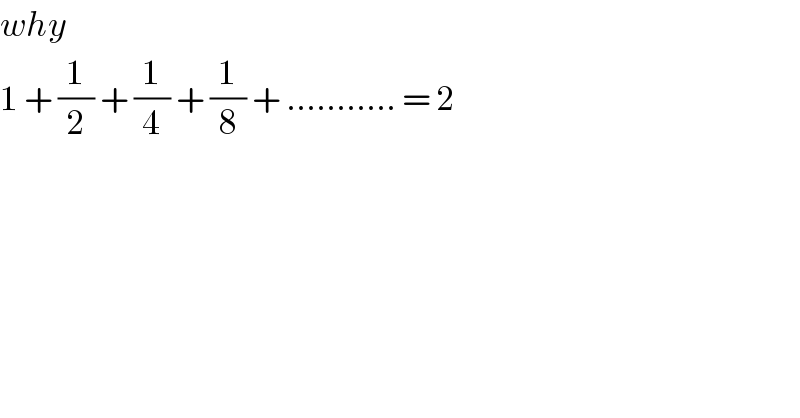
$${why} \\ $$$$\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\:+\:………..\:=\:\mathrm{2} \\ $$$$ \\ $$
Answered by FilupSmith last updated on 24/Apr/16
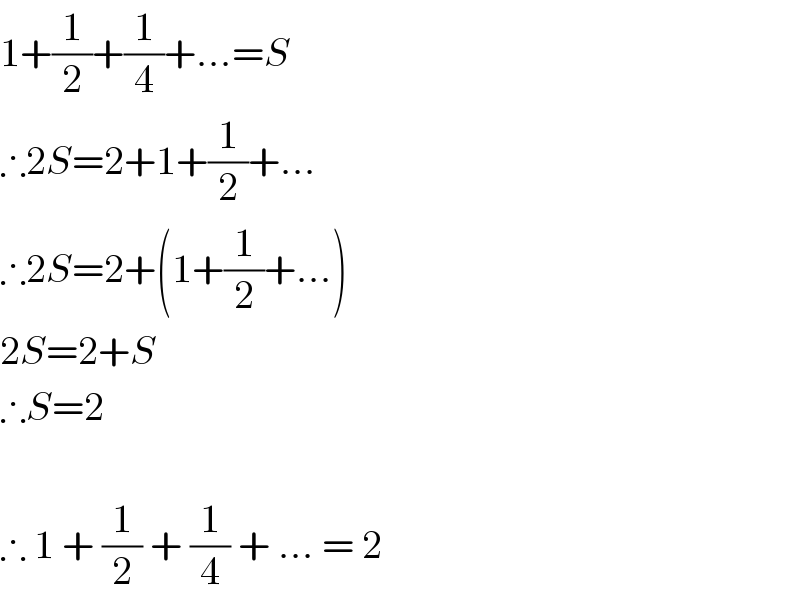
$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+…={S} \\ $$$$\therefore\mathrm{2}{S}=\mathrm{2}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+… \\ $$$$\therefore\mathrm{2}{S}=\mathrm{2}+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+…\right) \\ $$$$\mathrm{2}{S}=\mathrm{2}+{S} \\ $$$$\therefore{S}=\mathrm{2} \\ $$$$ \\ $$$$\therefore\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:…\:=\:\mathrm{2} \\ $$
Commented by 1771727373 last updated on 24/Apr/16
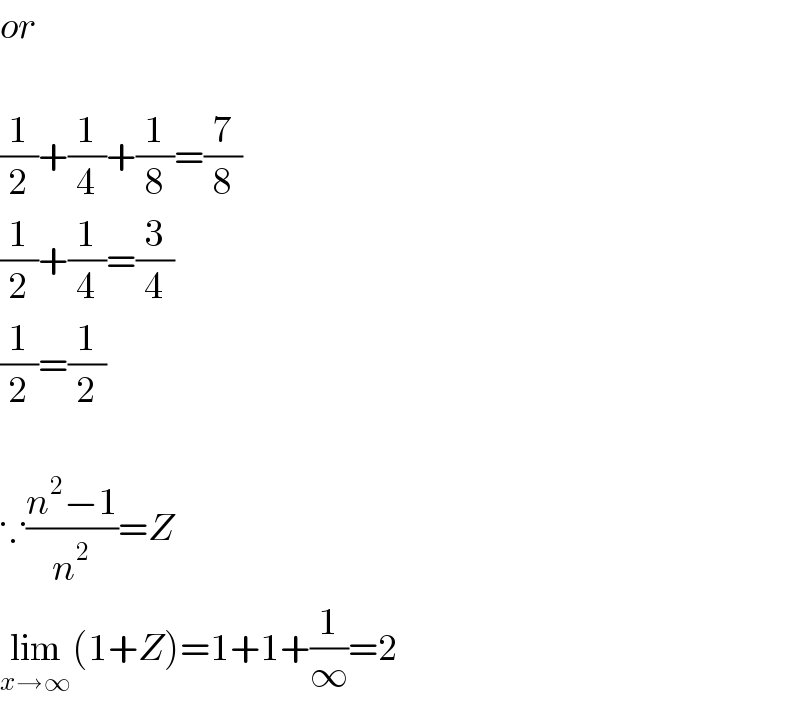
$${or} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\because\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} }={Z} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+{Z}\right)=\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}}{\infty}=\mathrm{2} \\ $$
Commented by FilupSmith last updated on 25/Apr/16

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{correct}. \\ $$$$\mathrm{The}\:\mathrm{limit}\:\mathrm{only}\:\mathrm{shows}\:\mathrm{its}\:\mathrm{divergance}. \\ $$$$\mathrm{Not}\:\mathrm{its}\:\mathrm{sum} \\ $$
Commented by prakash jain last updated on 26/Apr/16
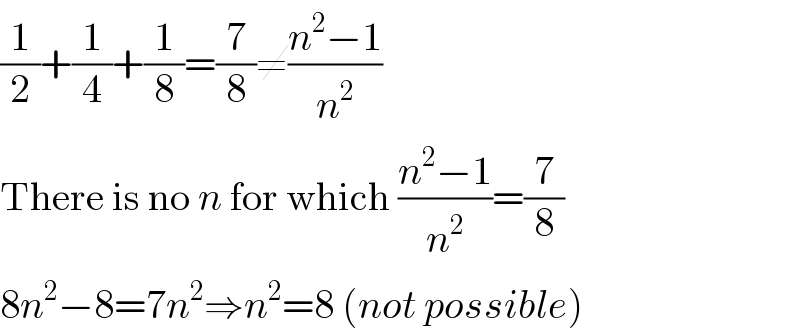
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{7}}{\mathrm{8}}\neq\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:{n}\:\mathrm{for}\:\mathrm{which}\:\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$\mathrm{8}{n}^{\mathrm{2}} −\mathrm{8}=\mathrm{7}{n}^{\mathrm{2}} \Rightarrow{n}^{\mathrm{2}} =\mathrm{8}\:\left({not}\:{possible}\right) \\ $$
Commented by 1771727373 last updated on 27/Apr/16
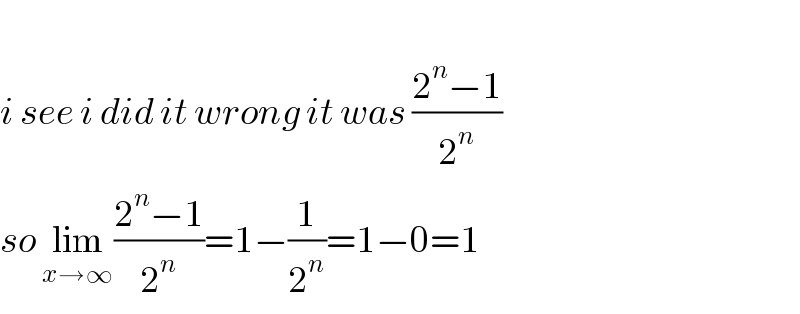
$$ \\ $$$${i}\:{see}\:{i}\:{did}\:{it}\:{wrong}\:{it}\:{was}\:\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${so}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{1}−\mathrm{0}=\mathrm{1} \\ $$
