Question Number 11571 by Nayon last updated on 28/Mar/17
![why ((d[f{g(x)}])/dx)=((df[{g(x)}])/(dg(x))).((dg(x))/dx)?](https://www.tinkutara.com/question/Q11571.png)
$${why}\:\:\:\frac{{d}\left[{f}\left\{{g}\left({x}\right)\right\}\right]}{{dx}}=\frac{{df}\left[\left\{{g}\left({x}\right)\right\}\right]}{{dg}\left({x}\right)}.\frac{{dg}\left({x}\right)}{{dx}}? \\ $$
Answered by mrW1 last updated on 28/Mar/17
![y=f(u) u=g(x) (dy/dx)=(dy/du)×(du/dx) ⇒ ((d[f{g(x)}])/dx)=((df[{g(x)}])/(dg(x))).((dg(x))/dx)](https://www.tinkutara.com/question/Q11576.png)
$${y}={f}\left({u}\right) \\ $$$${u}={g}\left({x}\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{du}}×\frac{{du}}{{dx}} \\ $$$$\Rightarrow\:\frac{{d}\left[{f}\left\{{g}\left({x}\right)\right\}\right]}{{dx}}=\frac{{df}\left[\left\{{g}\left({x}\right)\right\}\right]}{{dg}\left({x}\right)}.\frac{{dg}\left({x}\right)}{{dx}} \\ $$$$ \\ $$
Commented by mrW1 last updated on 28/Mar/17
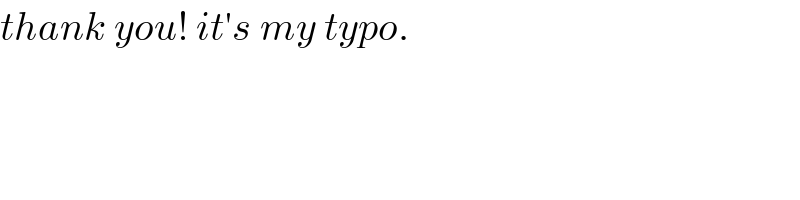
$${thank}\:{you}!\:{it}'{s}\:{my}\:{typo}. \\ $$
Answered by Joel576 last updated on 28/Mar/17

$$\mathrm{Chain}\:\mathrm{rule} \\ $$
Commented by linkelly0615 last updated on 29/Mar/17

$${uh}… \\ $$$${sorry}\:… \\ $$$${I}\:{flagged}\:{a}\:{wrong}\:{post}. \\ $$
