Question Number 6987 by sarathon last updated on 04/Aug/16

$${why}\:\:{e}^{{ln}\frac{\mathrm{1}}{\mathrm{3}}} \:{to}\:{be}\:\frac{\mathrm{1}}{\mathrm{3}}??? \\ $$$$ \\ $$$$ \\ $$
Commented by FilupSmith last updated on 04/Aug/16

$${a}^{\mathrm{log}_{{a}} \left({b}\right)} ={b} \\ $$
Answered by FilupSmith last updated on 04/Aug/16
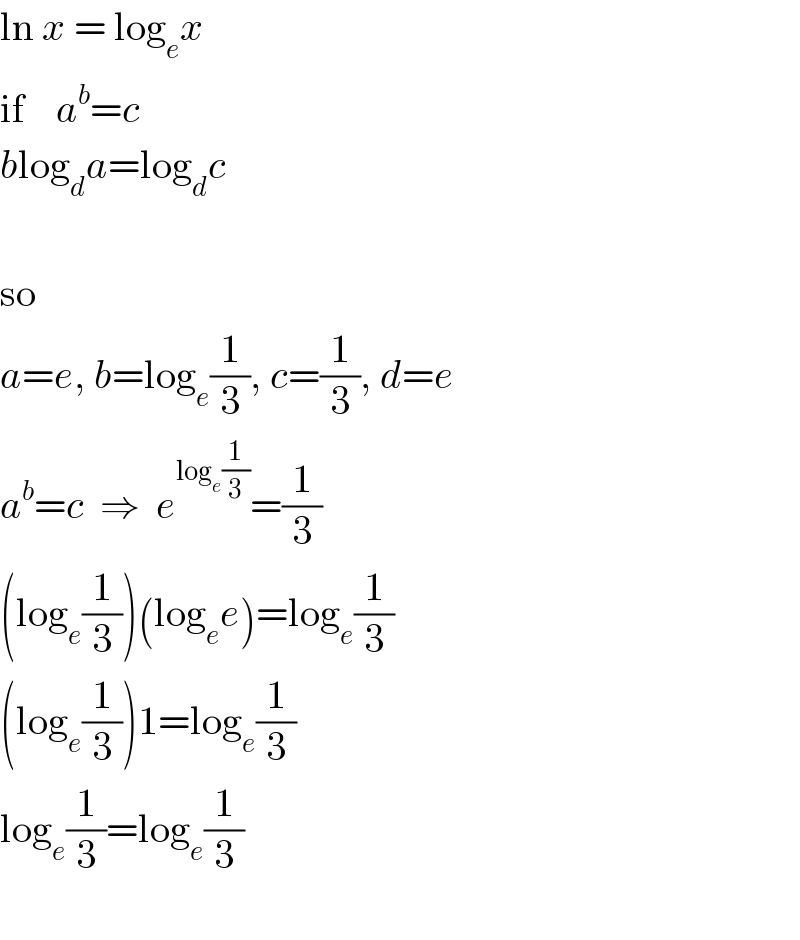
$$\mathrm{ln}\:{x}\:=\:\mathrm{log}_{{e}} {x} \\ $$$$\mathrm{if}\:\:\:\:{a}^{{b}} ={c} \\ $$$${b}\mathrm{log}_{{d}} {a}=\mathrm{log}_{{d}} {c} \\ $$$$ \\ $$$$\mathrm{so} \\ $$$${a}={e},\:{b}=\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}},\:{c}=\frac{\mathrm{1}}{\mathrm{3}},\:{d}={e} \\ $$$${a}^{{b}} ={c}\:\:\Rightarrow\:\:{e}^{\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{log}_{{e}} {e}\right)=\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left(\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}}\right)\mathrm{1}=\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}}=\mathrm{log}_{{e}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$
