Question Number 2762 by Rasheed Soomro last updated on 26/Nov/15

$${Without}\:{using}\:\underset{−} {{induction}}\:{o}\underset{−} {{r}\:\:{arithmatic}\:{series}−{concept}\:\:\:} \\ $$$$\:{prove}\:{the}\:{following}: \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Answered by prakash jain last updated on 26/Nov/15
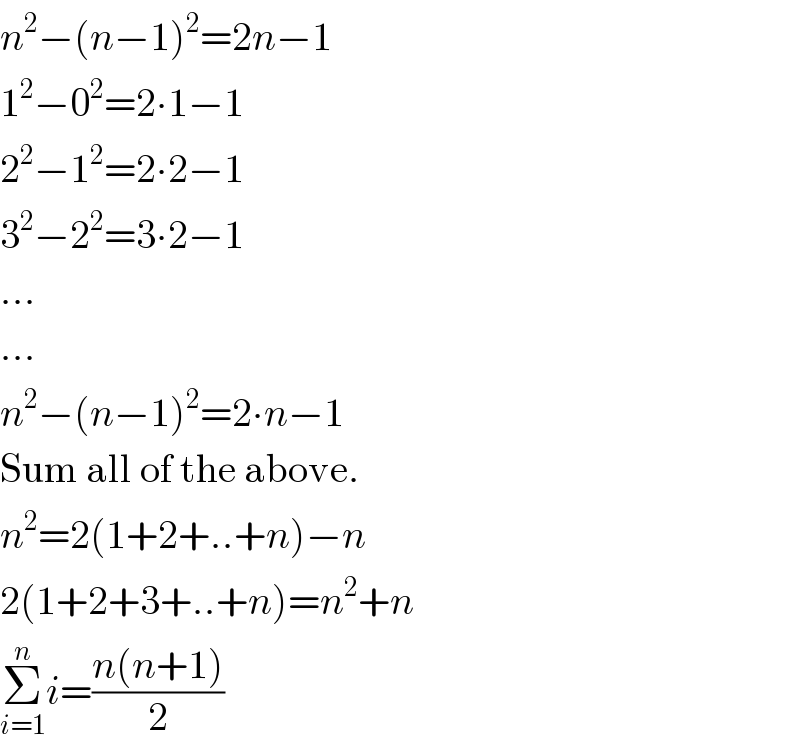
$${n}^{\mathrm{2}} −\left({n}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}{n}−\mathrm{1} \\ $$$$\mathrm{1}^{\mathrm{2}} −\mathrm{0}^{\mathrm{2}} =\mathrm{2}\centerdot\mathrm{1}−\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} =\mathrm{2}\centerdot\mathrm{2}−\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} =\mathrm{3}\centerdot\mathrm{2}−\mathrm{1} \\ $$$$… \\ $$$$… \\ $$$${n}^{\mathrm{2}} −\left({n}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\centerdot{n}−\mathrm{1} \\ $$$$\mathrm{Sum}\:\mathrm{all}\:\mathrm{of}\:\mathrm{the}\:\mathrm{above}. \\ $$$${n}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}+\mathrm{2}+..+{n}\right)−{n} \\ $$$$\mathrm{2}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+..+{n}\right)={n}^{\mathrm{2}} +{n} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 27/Nov/15

$$\mathcal{T}{hank}\mathcal{S}! \\ $$
