Question Number 10129 by Tawakalitu ayo mi last updated on 26/Jan/17
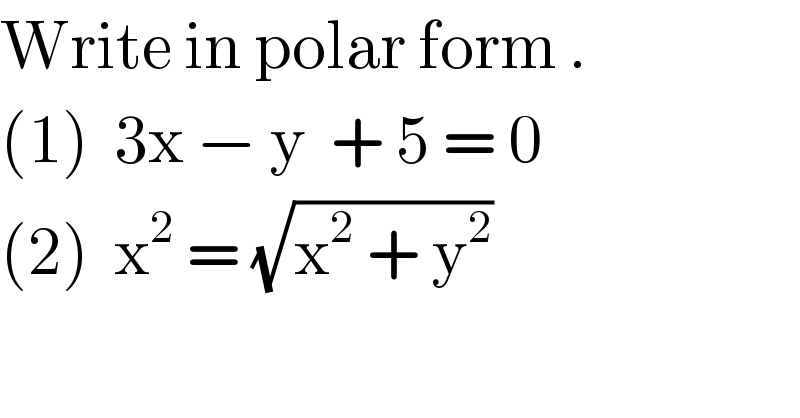
$$\mathrm{Write}\:\mathrm{in}\:\mathrm{polar}\:\mathrm{form}\:. \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{3x}\:−\:\mathrm{y}\:\:+\:\mathrm{5}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{x}^{\mathrm{2}} \:=\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} } \\ $$
Answered by icyfalcon999 last updated on 26/Jan/17
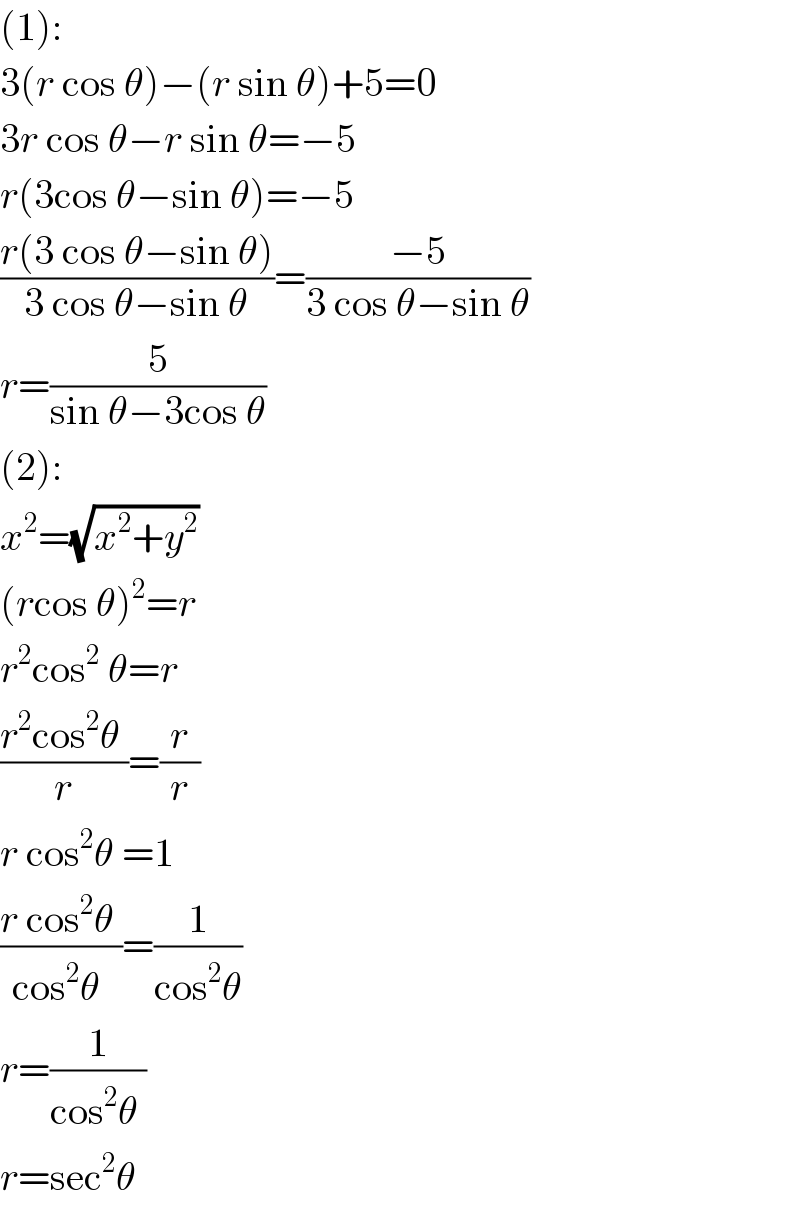
$$\left(\mathrm{1}\right): \\ $$$$\mathrm{3}\left({r}\:\mathrm{cos}\:\theta\right)−\left({r}\:\mathrm{sin}\:\theta\right)+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{3}{r}\:\mathrm{cos}\:\theta−{r}\:\mathrm{sin}\:\theta=−\mathrm{5} \\ $$$${r}\left(\mathrm{3cos}\:\theta−\mathrm{sin}\:\theta\right)=−\mathrm{5} \\ $$$$\frac{{r}\left(\mathrm{3}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)}{\mathrm{3}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta}=\frac{−\mathrm{5}}{\mathrm{3}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta} \\ $$$${r}=\frac{\mathrm{5}}{\mathrm{sin}\:\theta−\mathrm{3cos}\:\theta} \\ $$$$\left(\mathrm{2}\right): \\ $$$${x}^{\mathrm{2}} =\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\left({r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} ={r} \\ $$$${r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta={r} \\ $$$$\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\:}{{r}}=\frac{{r}}{{r}} \\ $$$${r}\:\mathrm{cos}^{\mathrm{2}} \theta\:=\mathrm{1} \\ $$$$\frac{{r}\:\mathrm{cos}^{\mathrm{2}} \theta\:}{\mathrm{cos}^{\mathrm{2}} \theta\:}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta\:} \\ $$$${r}=\mathrm{sec}^{\mathrm{2}} \theta\: \\ $$
Commented by Tawakalitu ayo mi last updated on 26/Jan/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
