Write-the-next-three-terms-1-3-7-8-3-

Question Number 141197 by paulpadas last updated on 16/May/21

$${Write}\:{the}\:{next}\:{three}\:{terms}\:\mathrm{1},\:\frac{\mathrm{3}}{\mathrm{7}},\:\frac{\mathrm{8}}{\mathrm{3}},\:\_\_\_,\:\_\_\_,\:\_\_\_,\:… \\ $$

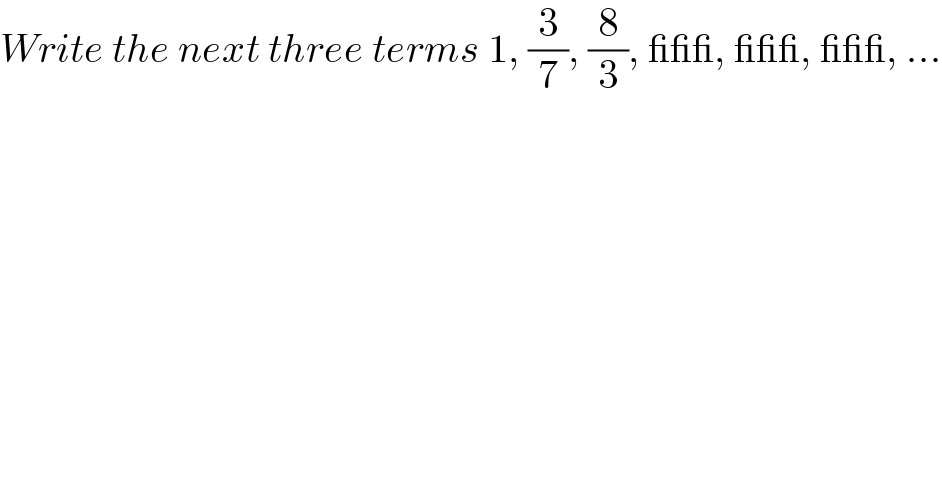
Answered by MJS_new last updated on 16/May/21

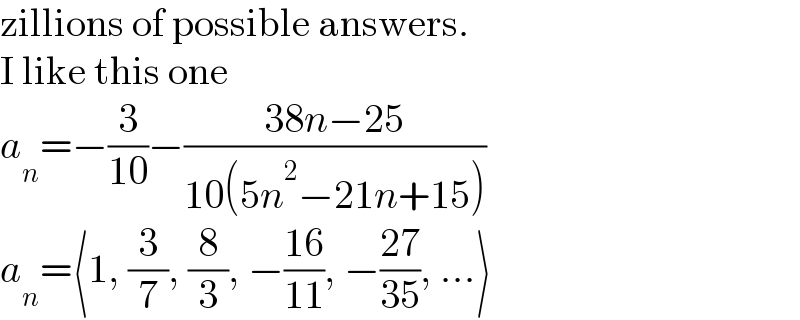
zillions of possible answers. I like this one a_n =−(3/(10))−((38n−25)/(10(5n^2 −21n+15))) a_n =⟨1, (3/7), (8/3), −((16)/(11)), −((27)/(35)), ...⟩

$$\mathrm{zillions}\:\mathrm{of}\:\mathrm{possible}\:\mathrm{answers}. \\ $$$$\mathrm{I}\:\mathrm{like}\:\mathrm{this}\:\mathrm{one} \\ $$$${a}_{{n}} =−\frac{\mathrm{3}}{\mathrm{10}}−\frac{\mathrm{38}{n}−\mathrm{25}}{\mathrm{10}\left(\mathrm{5}{n}^{\mathrm{2}} −\mathrm{21}{n}+\mathrm{15}\right)} \\ $$$${a}_{{n}} =\langle\mathrm{1},\:\frac{\mathrm{3}}{\mathrm{7}},\:\frac{\mathrm{8}}{\mathrm{3}},\:−\frac{\mathrm{16}}{\mathrm{11}},\:−\frac{\mathrm{27}}{\mathrm{35}},\:…\rangle \\ $$

Commented by Ar Brandon last updated on 16/May/21

Hi ! Nice week-end Sir ! ��

Commented by MJS_new last updated on 16/May/21

for you too!

Commented by Ar Brandon last updated on 16/May/21

I finally got a chance to apply the method you taught me last year. First on Q140789 and then Q140976 Did you see it, Sir ?

$$\:\mathrm{I}\:\mathrm{finally}\:\mathrm{got}\:\mathrm{a}\:\mathrm{chance}\:\mathrm{to}\:\mathrm{apply}\:\mathrm{the}\:\mathrm{method}\:\mathrm{you}\:\mathrm{taught} \\ $$$$\mathrm{me}\:\mathrm{last}\:\mathrm{year}.\:\mathrm{First}\:\mathrm{on}\:\mathrm{Q140789}\:\mathrm{and}\:\mathrm{then}\:\mathrm{Q140976} \\ $$$$\mathrm{Did}\:\mathrm{you}\:\mathrm{see}\:\mathrm{it},\:\mathrm{Sir}\:? \\ $$

Commented by Ar Brandon last updated on 16/May/21