Question Number 8750 by tawakalitu last updated on 25/Oct/16
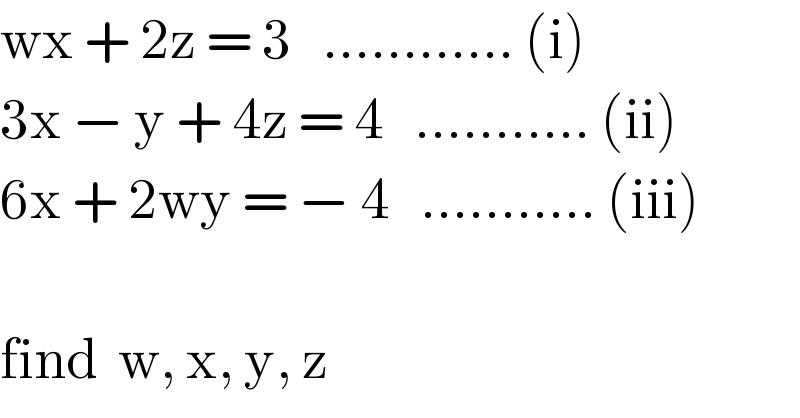
$$\mathrm{wx}\:+\:\mathrm{2z}\:=\:\mathrm{3}\:\:\:…………\:\left(\mathrm{i}\right) \\ $$$$\mathrm{3x}\:−\:\mathrm{y}\:+\:\mathrm{4z}\:=\:\mathrm{4}\:\:\:………..\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{6x}\:+\:\mathrm{2wy}\:=\:−\:\mathrm{4}\:\:\:………..\:\left(\mathrm{iii}\right) \\ $$$$ \\ $$$$\mathrm{find}\:\:\mathrm{w},\:\mathrm{x},\:\mathrm{y},\:\mathrm{z} \\ $$
Commented by Rasheed Soomro last updated on 26/Oct/16

$$\mathrm{More}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{required}\:\mathrm{to}\:\mathrm{determine} \\ $$$$\mathrm{all}\:\mathrm{w},\:\mathrm{x},\:\mathrm{y},\:\mathrm{z}\:\mathrm{in}\:\mathrm{numbers}. \\ $$
Commented by tawakalitu last updated on 26/Oct/16
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by Rasheed Soomro last updated on 26/Oct/16

$$\mathrm{wx}\:+\:\mathrm{2z}\:=\:\mathrm{3}\:\:\:…………\:\left(\mathrm{i}\right) \\ $$$$\mathrm{3x}\:−\:\mathrm{y}\:+\:\mathrm{4z}\:=\:\mathrm{4}\:\:\:………..\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{6x}\:+\:\mathrm{2wy}\:=\:−\:\mathrm{4}\:\:\:………..\:\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{iii}\right)\Rightarrow\mathrm{3x}=−\mathrm{2}−\mathrm{wy}………………\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\mathrm{3x}=\mathrm{y}−\mathrm{4z}+\mathrm{4}…………………….\left(\mathrm{v}\right) \\ $$$$\left(\mathrm{iv}\right),\left(\mathrm{v}\right)\Rightarrow−\mathrm{2}−\mathrm{wy}=\mathrm{y}−\mathrm{4z}+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{y}+\mathrm{wy}=−\mathrm{6}+\mathrm{4z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{y}=\frac{−\mathrm{6}+\mathrm{4z}}{\mathrm{1}+\mathrm{w}}…………….\mathrm{A} \\ $$$$\left(\mathrm{i}\right),\left(\mathrm{iv}\right)\Rightarrow\:\:\mathrm{x}=\frac{\mathrm{3}−\mathrm{2z}}{\mathrm{w}}………………….\mathrm{B} \\ $$$$\bullet\mathrm{Insufficient}\:\mathrm{data}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{w},\mathrm{x},\mathrm{y},\mathrm{z} \\ $$$$\:\:\:\:\:\mathrm{in}\:\mathrm{numbers}. \\ $$$$\bullet\mathrm{We}\:\mathrm{can}\:\mathrm{only}\:\mathrm{determine}\:\mathrm{any}\:\mathrm{two}\:\mathrm{of}\:\mathrm{w},\mathrm{x},\mathrm{y},\mathrm{z} \\ $$$$\:\:\:\:\:\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{remaining}\:\mathrm{two}. \\ $$$$\bullet\mathrm{In}\:\mathrm{A}\:\mathrm{and}\:\:\mathrm{B}\:\mathrm{we}'\mathrm{ve}\:\mathrm{determined}\:\mathrm{x}\:\mathrm{and}\:\:\mathrm{y} \\ $$$$\:\:\:\:\:\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{w}\:\mathrm{and}\:\:\mathrm{z}. \\ $$$$ \\ $$
Commented by tawakalitu last updated on 26/Oct/16
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
