Question Number 8740 by 123456 last updated on 25/Oct/16
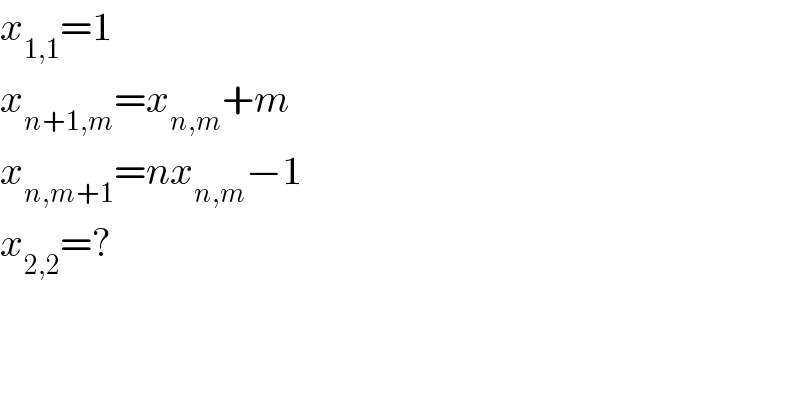
$${x}_{\mathrm{1},\mathrm{1}} =\mathrm{1} \\ $$$${x}_{{n}+\mathrm{1},{m}} ={x}_{{n},{m}} +{m} \\ $$$${x}_{{n},{m}+\mathrm{1}} ={nx}_{{n},{m}} −\mathrm{1} \\ $$$${x}_{\mathrm{2},\mathrm{2}} =? \\ $$
Commented by Yozzias last updated on 25/Oct/16
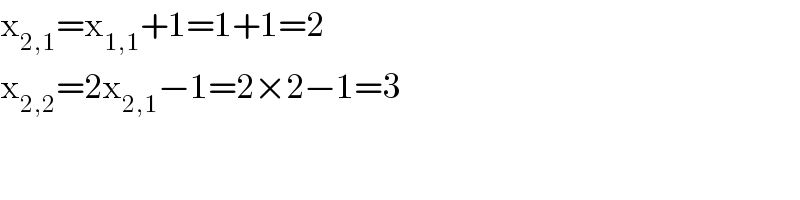
$$\mathrm{x}_{\mathrm{2},\mathrm{1}} =\mathrm{x}_{\mathrm{1},\mathrm{1}} +\mathrm{1}=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$$\mathrm{x}_{\mathrm{2},\mathrm{2}} =\mathrm{2x}_{\mathrm{2},\mathrm{1}} −\mathrm{1}=\mathrm{2}×\mathrm{2}−\mathrm{1}=\mathrm{3} \\ $$
Commented by prakash jain last updated on 25/Oct/16

$$\mathrm{General}\:\mathrm{formula}\:\mathrm{for}\:{x}_{{n},{m}} ? \\ $$
