Menu Close

x-1-16-1-x-1-8-1-x-1-4-1-x-1-2-1-

Tinku Tara 0 Comments
Pin




Question Number 10005 by konen last updated on 20/Jan/17
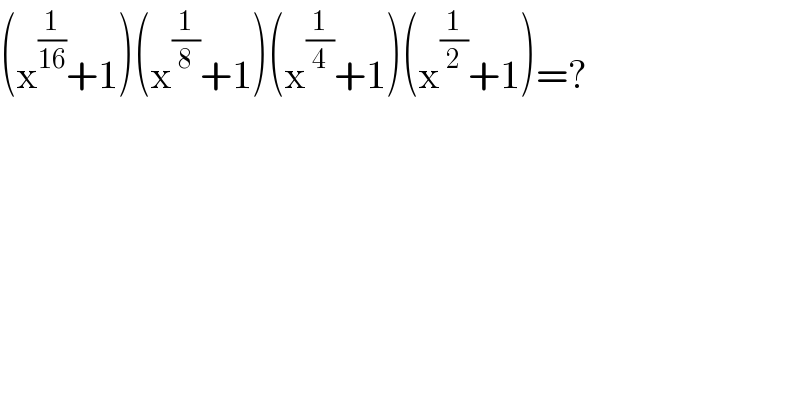
(x^(1/(16)) +1)(x^(1/8) +1)(x^(1/4) +1)(x^(1/2) +1)=?
$$\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right)=? \\ $$
Answered by mrW1 last updated on 21/Jan/17
P=(x^(1/(16)) +1)(x^(1/8) +1)(x^(1/4) +1)(x^(1/2) +1) if x=1: P=(1+1)^4 =2^4 =16 if x≠1: (x^(1/(16)) −1)P=(x^(1/(16)) −1)(x^(1/(16)) +1)(x^(1/8) +1)(x^(1/4) +1)(x^(1/2) +1) (x^(1/(16)) −1)P=(x^(1/8) −1)(x^(1/8) +1)(x^(1/4) +1)(x^(1/2) +1) (x^(1/(16)) −1)P=(x^(1/4) −1)(x^(1/4) +1)(x^(1/2) +1) (x^(1/(16)) −1)P=(x^(1/2) −1)(x^(1/2) +1) (x^(1/(16)) −1)P=(x−1) P=((x−1)/(x^(1/(16)) −1))
$${P}=\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right) \\ $$$$ \\ $$$${if}\:{x}=\mathrm{1}: \\ $$$${P}=\left(\mathrm{1}+\mathrm{1}\right)^{\mathrm{4}} =\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$$$ \\ $$$${if}\:{x}\neq\mathrm{1}: \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right){P}=\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{16}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right) \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right){P}=\left({x}^{\frac{\mathrm{1}}{\mathrm{8}}} −\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{8}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right) \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right){P}=\left({x}^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right) \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right){P}=\left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)\left(\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}\right) \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}\right){P}=\left({x}−\mathrm{1}\right) \\ $$$${P}=\frac{{x}−\mathrm{1}}{{x}^{\frac{\mathrm{1}}{\mathrm{16}}} −\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *