Question Number 75753 by Emmanuel_N last updated on 16/Dec/19
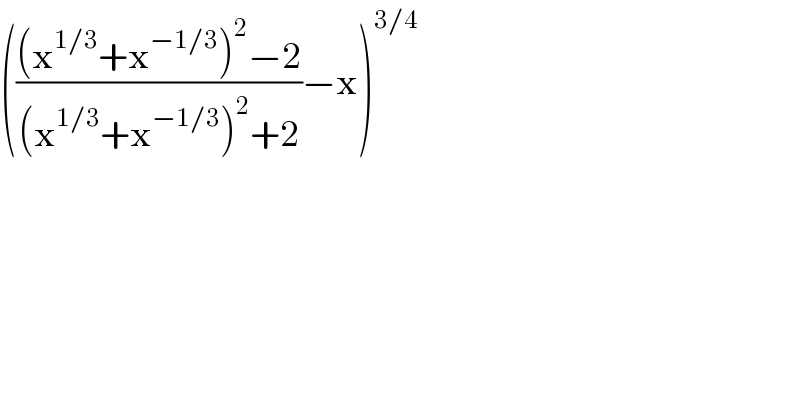
$$\left(\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{x}^{−\mathrm{1}/\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{2}}{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{x}^{−\mathrm{1}/\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{2}}−\mathrm{x}\right)^{\mathrm{3}/\mathrm{4}} \\ $$
Answered by $@ty@m123 last updated on 16/Dec/19
![Let y=x^(1/3) =[(((y+(1/y))^2 −2)/((y−(1/y))^2 +2)) −x]^(3/4) =[((y^2 +(1/y^2 ))/(y^2 +(1/y^2 ))) −x]^(3/4) =(1−x)^(3/4)](https://www.tinkutara.com/question/Q75761.png)
$${Let}\:{y}={x}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\left[\frac{\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}}{\left({y}−\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} +\mathrm{2}}\:−{x}\right]^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\left[\frac{{y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }}{{y}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }}\:−{x}\right]^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 17/Dec/19
![but the original question is =[(((y+(1/y))^2 −2)/((y+(1/y))^2 +2)) −x]^(3/4)](https://www.tinkutara.com/question/Q75785.png)
$${but}\:{the}\:{original}\:{question}\:{is} \\ $$$$=\left[\frac{\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} −\mathrm{2}}{\left({y}+\frac{\mathrm{1}}{{y}}\right)^{\mathrm{2}} +\mathrm{2}}\:−{x}\right]^{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$
