Question Number 138240 by bobhans last updated on 11/Apr/21
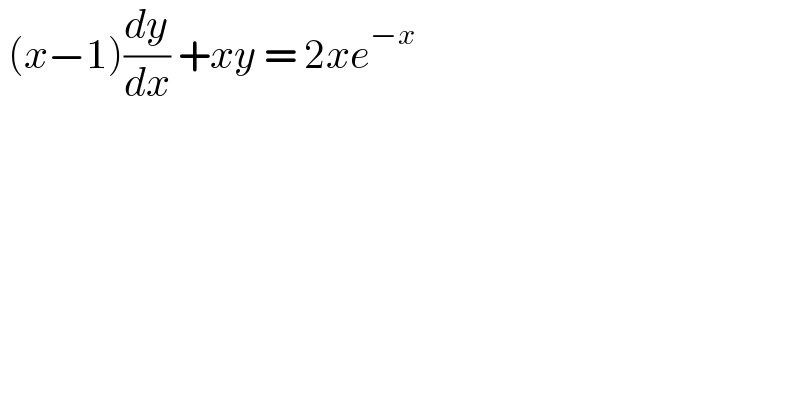
$$\:\left({x}−\mathrm{1}\right)\frac{{dy}}{{dx}}\:+{xy}\:=\:\mathrm{2}{xe}^{−{x}} \\ $$
Answered by EDWIN88 last updated on 11/Apr/21
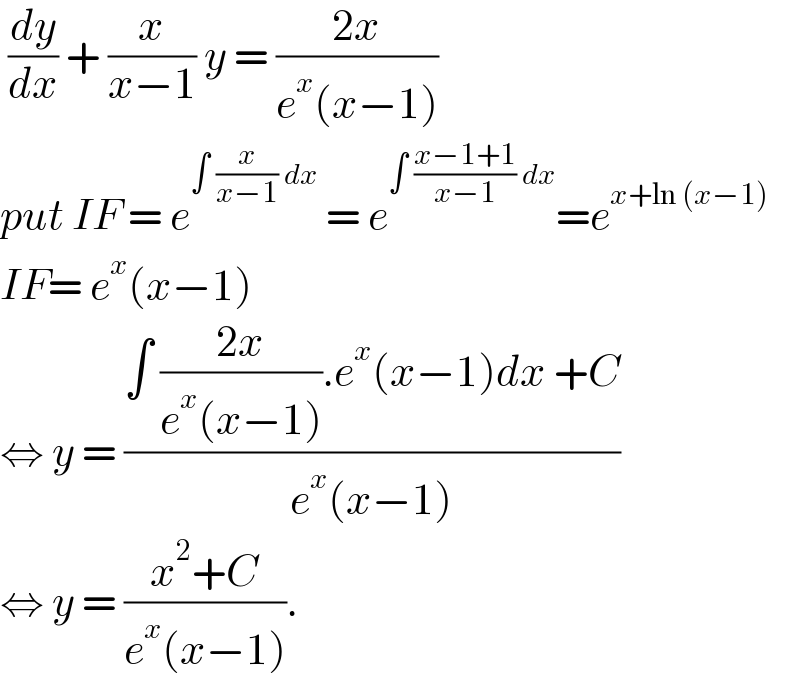
$$\:\frac{{dy}}{{dx}}\:+\:\frac{{x}}{{x}−\mathrm{1}}\:{y}\:=\:\frac{\mathrm{2}{x}}{{e}^{{x}} \left({x}−\mathrm{1}\right)} \\ $$$${put}\:{IF}\:=\:{e}^{\int\:\frac{{x}}{{x}−\mathrm{1}}\:{dx}} \:=\:{e}^{\int\:\frac{{x}−\mathrm{1}+\mathrm{1}}{{x}−\mathrm{1}}\:{dx}} ={e}^{{x}+\mathrm{ln}\:\left({x}−\mathrm{1}\right)} \\ $$$${IF}=\:{e}^{{x}} \left({x}−\mathrm{1}\right) \\ $$$$\Leftrightarrow\:{y}\:=\:\frac{\int\:\frac{\mathrm{2}{x}}{{e}^{{x}} \left({x}−\mathrm{1}\right)}.{e}^{{x}} \left({x}−\mathrm{1}\right){dx}\:+{C}}{{e}^{{x}} \left({x}−\mathrm{1}\right)} \\ $$$$\Leftrightarrow\:{y}\:=\:\frac{{x}^{\mathrm{2}} +{C}}{{e}^{{x}} \left({x}−\mathrm{1}\right)}.\: \\ $$
Answered by physicstutes last updated on 11/Apr/21
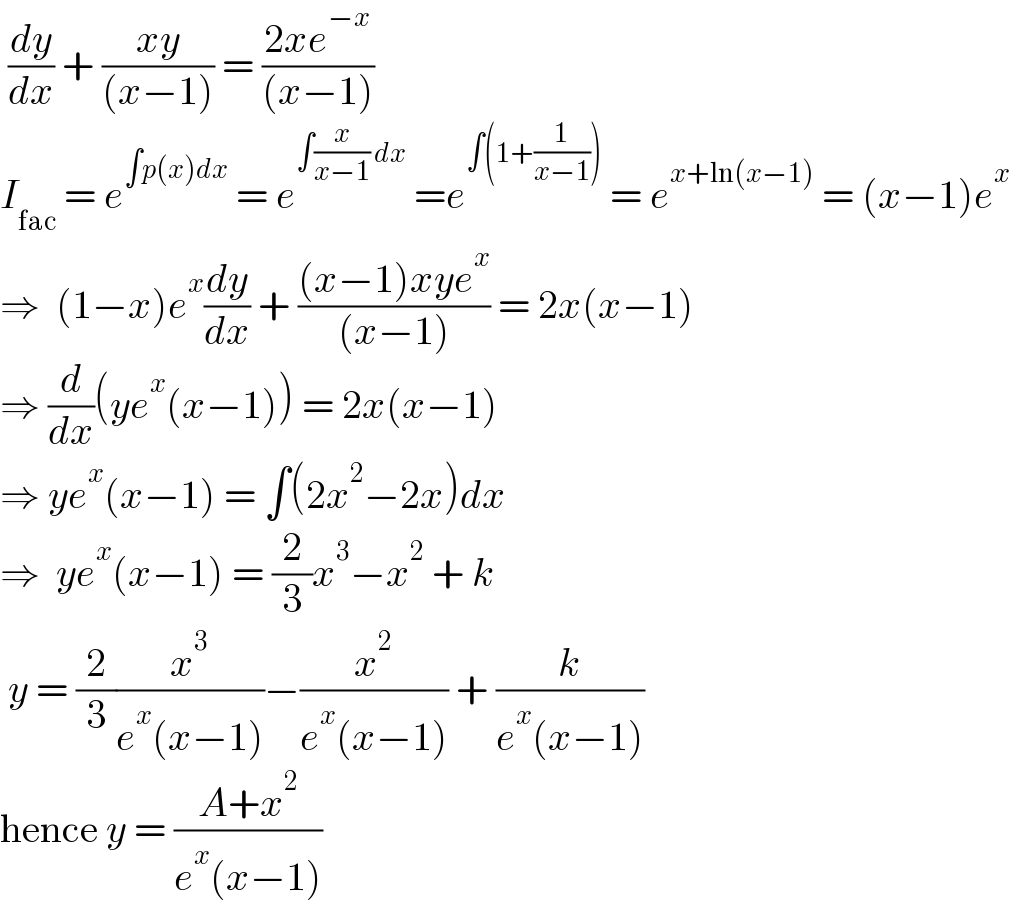
$$\:\frac{{dy}}{{dx}}\:+\:\frac{{xy}}{\left({x}−\mathrm{1}\right)}\:=\:\frac{\mathrm{2}{xe}^{−{x}} }{\left({x}−\mathrm{1}\right)} \\ $$$${I}_{\mathrm{fac}} \:=\:{e}^{\int{p}\left({x}\right){dx}} \:=\:{e}^{\int\frac{{x}}{{x}−\mathrm{1}}\:{dx}} \:={e}^{\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)} \:=\:{e}^{{x}+\mathrm{ln}\left({x}−\mathrm{1}\right)} \:=\:\left({x}−\mathrm{1}\right){e}^{{x}} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{x}\right){e}^{{x}} \frac{{dy}}{{dx}}\:+\:\frac{\left({x}−\mathrm{1}\right){xye}^{{x}} }{\left({x}−\mathrm{1}\right)}\:=\:\mathrm{2}{x}\left({x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\frac{{d}}{{dx}}\left({ye}^{{x}} \left({x}−\mathrm{1}\right)\right)\:=\:\mathrm{2}{x}\left({x}−\mathrm{1}\right) \\ $$$$\Rightarrow\:{ye}^{{x}} \left({x}−\mathrm{1}\right)\:=\:\int\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\right){dx} \\ $$$$\Rightarrow\:\:{ye}^{{x}} \left({x}−\mathrm{1}\right)\:=\:\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} \:+\:{k} \\ $$$$\:{y}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\frac{{x}^{\mathrm{3}} }{{e}^{{x}} \left({x}−\mathrm{1}\right)}−\frac{{x}^{\mathrm{2}} }{{e}^{{x}} \left({x}−\mathrm{1}\right)}\:+\:\frac{{k}}{{e}^{{x}} \left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{hence}\:{y}\:=\:\frac{{A}+{x}^{\mathrm{2}} }{{e}^{{x}} \left({x}−\mathrm{1}\right)} \\ $$
Answered by mathmax by abdo last updated on 11/Apr/21
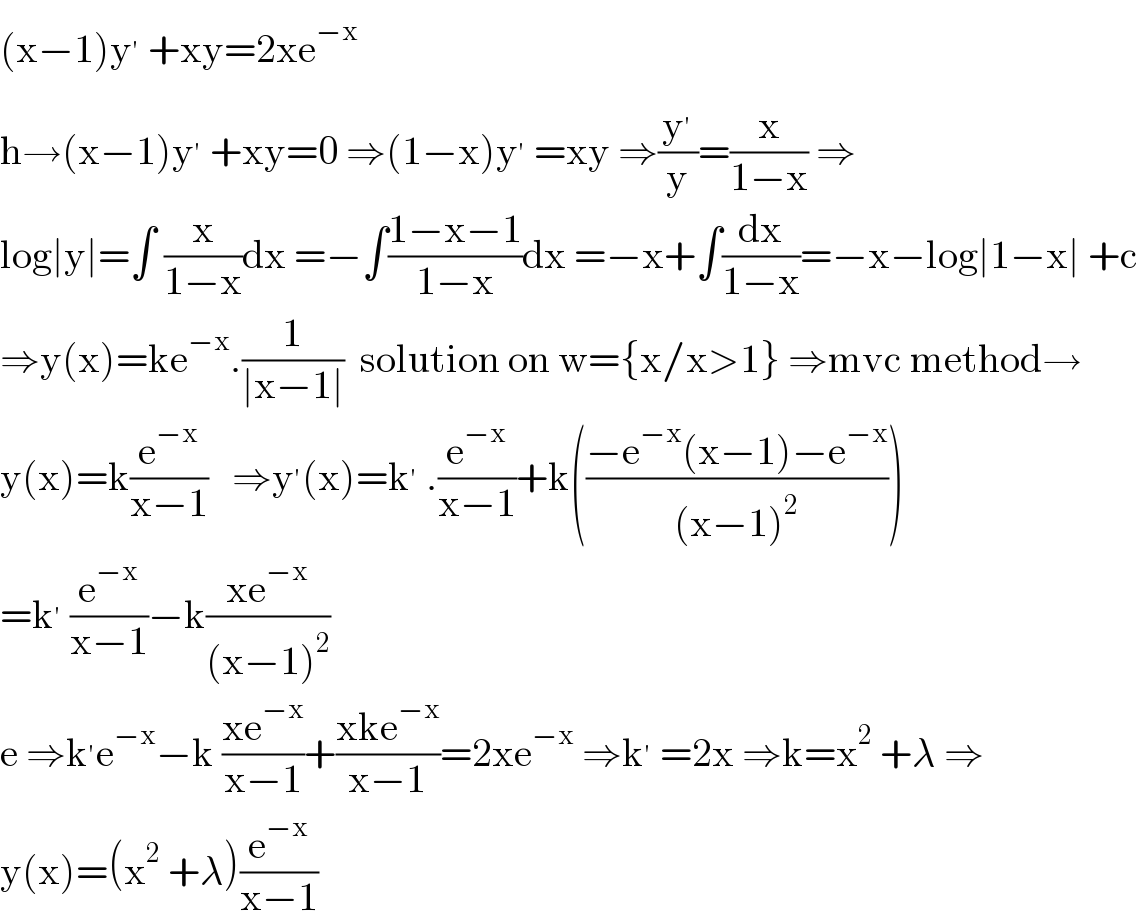
$$\left(\mathrm{x}−\mathrm{1}\right)\mathrm{y}^{'} \:+\mathrm{xy}=\mathrm{2xe}^{−\mathrm{x}} \\ $$$$\mathrm{h}\rightarrow\left(\mathrm{x}−\mathrm{1}\right)\mathrm{y}^{'} \:+\mathrm{xy}=\mathrm{0}\:\Rightarrow\left(\mathrm{1}−\mathrm{x}\right)\mathrm{y}^{'} \:=\mathrm{xy}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}=\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{log}\mid\mathrm{y}\mid=\int\:\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=−\int\frac{\mathrm{1}−\mathrm{x}−\mathrm{1}}{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=−\mathrm{x}+\int\frac{\mathrm{dx}}{\mathrm{1}−\mathrm{x}}=−\mathrm{x}−\mathrm{log}\mid\mathrm{1}−\mathrm{x}\mid\:+\mathrm{c} \\ $$$$\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{ke}^{−\mathrm{x}} .\frac{\mathrm{1}}{\mid\mathrm{x}−\mathrm{1}\mid}\:\:\mathrm{solution}\:\mathrm{on}\:\mathrm{w}=\left\{\mathrm{x}/\mathrm{x}>\mathrm{1}\right\}\:\Rightarrow\mathrm{mvc}\:\mathrm{method}\rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{k}\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}}\:\:\:\Rightarrow\mathrm{y}^{'} \left(\mathrm{x}\right)=\mathrm{k}^{'} \:.\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}}+\mathrm{k}\left(\frac{−\mathrm{e}^{−\mathrm{x}} \left(\mathrm{x}−\mathrm{1}\right)−\mathrm{e}^{−\mathrm{x}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\mathrm{k}^{'} \:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}}−\mathrm{k}\frac{\mathrm{xe}^{−\mathrm{x}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \mathrm{e}^{−\mathrm{x}} −\mathrm{k}\:\frac{\mathrm{xe}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}}+\frac{\mathrm{xke}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}}=\mathrm{2xe}^{−\mathrm{x}} \:\Rightarrow\mathrm{k}^{'} \:=\mathrm{2x}\:\Rightarrow\mathrm{k}=\mathrm{x}^{\mathrm{2}} \:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} \:+\lambda\right)\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}−\mathrm{1}} \\ $$
