Question Number 66290 by hmamarques1994@gmail.com last updated on 12/Aug/19
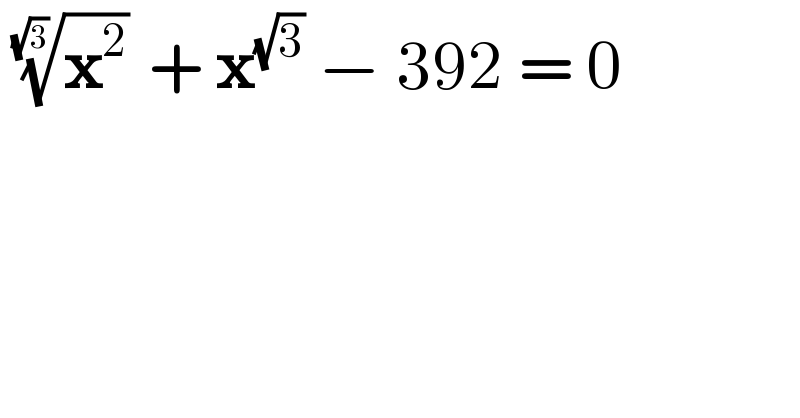
$$\:\sqrt[{\sqrt{\mathrm{3}}}]{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\:+\:\boldsymbol{\mathrm{x}}^{\sqrt{\mathrm{3}}} \:−\:\mathrm{392}\:=\:\mathrm{0} \\ $$
Answered by Tanmay chaudhury last updated on 12/Aug/19
![(x^2 )^(1/( (√3))) +x^(√3) −392=0 x^(2/( (√3) )) +x^((√3) ) −392=0 x^((2(√3))/3) +x^(√3) −392=0 a^(2/3) +a−392=0 b^2 +b^3 −392=0 [a^(1/3) =b →(x^((√3) ) )^(1/3) =b→x=(b)^(√3) ] b^2 −49+b^3 −343=0 (b+7)(b−7)+(b−7)(b^2 +7b+49)=0 (b−7)(b^2 +8b+56)=0 b=7→x=(7)^((√3) ) b^2 +8b+16+40≠0 (b+4)^2 +40≠0 if complex roots are allowed (b+4)^2 =i^2 ×40 b=−4±i(√(40)) x=(−4±i(√(40)) )^(√3)](https://www.tinkutara.com/question/Q66294.png)
$$\left({x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} +{x}^{\sqrt{\mathrm{3}}} −\mathrm{392}=\mathrm{0} \\ $$$${x}^{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}\:}} +{x}^{\sqrt{\mathrm{3}}\:} −\mathrm{392}=\mathrm{0} \\ $$$${x}^{\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}} +{x}^{\sqrt{\mathrm{3}}} \:−\mathrm{392}=\mathrm{0} \\ $$$${a}^{\frac{\mathrm{2}}{\mathrm{3}}} +{a}−\mathrm{392}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} +{b}^{\mathrm{3}} −\mathrm{392}=\mathrm{0}\:\:\:\left[{a}^{\frac{\mathrm{1}}{\mathrm{3}}} ={b}\:\rightarrow\left({x}^{\sqrt{\mathrm{3}}\:} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} ={b}\rightarrow{x}=\left({b}\right)^{\sqrt{\mathrm{3}}} \right] \\ $$$${b}^{\mathrm{2}} −\mathrm{49}+{b}^{\mathrm{3}} −\mathrm{343}=\mathrm{0} \\ $$$$\left({b}+\mathrm{7}\right)\left({b}−\mathrm{7}\right)+\left({b}−\mathrm{7}\right)\left({b}^{\mathrm{2}} +\mathrm{7}{b}+\mathrm{49}\right)=\mathrm{0} \\ $$$$\left({b}−\mathrm{7}\right)\left({b}^{\mathrm{2}} +\mathrm{8}{b}+\mathrm{56}\right)=\mathrm{0} \\ $$$${b}=\mathrm{7}\rightarrow{x}=\left(\mathrm{7}\right)^{\sqrt{\mathrm{3}}\:} \\ $$$${b}^{\mathrm{2}} +\mathrm{8}{b}+\mathrm{16}+\mathrm{40}\neq\mathrm{0} \\ $$$$\left({b}+\mathrm{4}\right)^{\mathrm{2}} +\mathrm{40}\neq\mathrm{0} \\ $$$${if}\:{complex}\:{roots}\:{are}\:{allowed} \\ $$$$\left({b}+\mathrm{4}\right)^{\mathrm{2}} ={i}^{\mathrm{2}} ×\mathrm{40} \\ $$$${b}=−\mathrm{4}\pm{i}\sqrt{\mathrm{40}}\: \\ $$$${x}=\left(−\mathrm{4}\pm{i}\sqrt{\mathrm{40}}\:\right)^{\sqrt{\mathrm{3}}} \\ $$
