Question Number 136841 by physicstutes last updated on 26/Mar/21

$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}\:{dx}\:=\:? \\ $$
Answered by Olaf last updated on 26/Mar/21
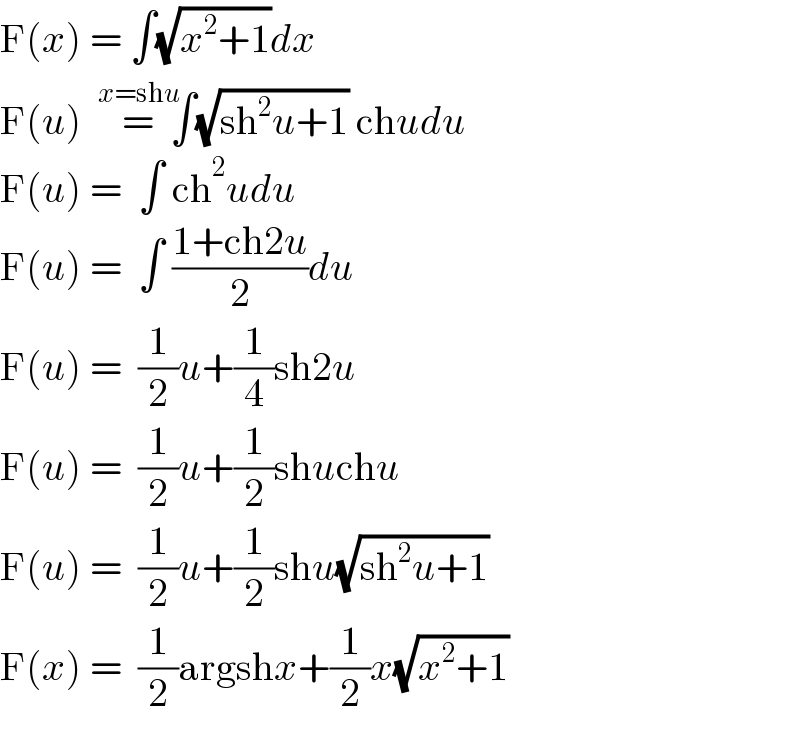
$$\mathrm{F}\left({x}\right)\:=\:\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\mathrm{F}\left({u}\right)\:\:\overset{{x}=\mathrm{sh}{u}} {=}\:\:\int\sqrt{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}}\:\mathrm{ch}{udu} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\:\int\:\mathrm{ch}^{\mathrm{2}} {udu} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\:\int\:\frac{\mathrm{1}+\mathrm{ch2}{u}}{\mathrm{2}}{du} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}{u}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh2}{u} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}{u}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}{u}\mathrm{ch}{u} \\ $$$$\mathrm{F}\left({u}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}{u}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}{u}\sqrt{\mathrm{sh}^{\mathrm{2}} {u}+\mathrm{1}} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{argsh}{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Answered by Olaf last updated on 26/Mar/21

$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{1}×\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\int{x}\frac{\mathrm{2}{x}}{\:\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\int\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{F}\left({x}\right)+\mathrm{argsh}{x} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{argsh}{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Answered by MJS_new last updated on 26/Mar/21
![∫(√(x^2 +1))dx= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))dt] =∫((t/4)+(1/(2t))+(1/(4t^3 )))dt=(t^2 /8)+((ln t)/2)−(1/(8t^2 ))= =((x(√(x^2 +1)))/2)+((ln (x+(√(x^2 +1))))/2)+C](https://www.tinkutara.com/question/Q136848.png)
$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dt}\right] \\ $$$$=\int\left(\frac{{t}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}{t}}+\frac{\mathrm{1}}{\mathrm{4}{t}^{\mathrm{3}} }\right){dt}=\frac{{t}^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{ln}\:{t}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}{t}^{\mathrm{2}} }= \\ $$$$=\frac{{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}}+\frac{\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\mathrm{2}}+{C} \\ $$
