Question Number 138250 by sahnaz last updated on 11/Apr/21

$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{6}\right)^{\mathrm{x}−\mathrm{2}} >\mathrm{1} \\ $$
Answered by bobhans last updated on 11/Apr/21
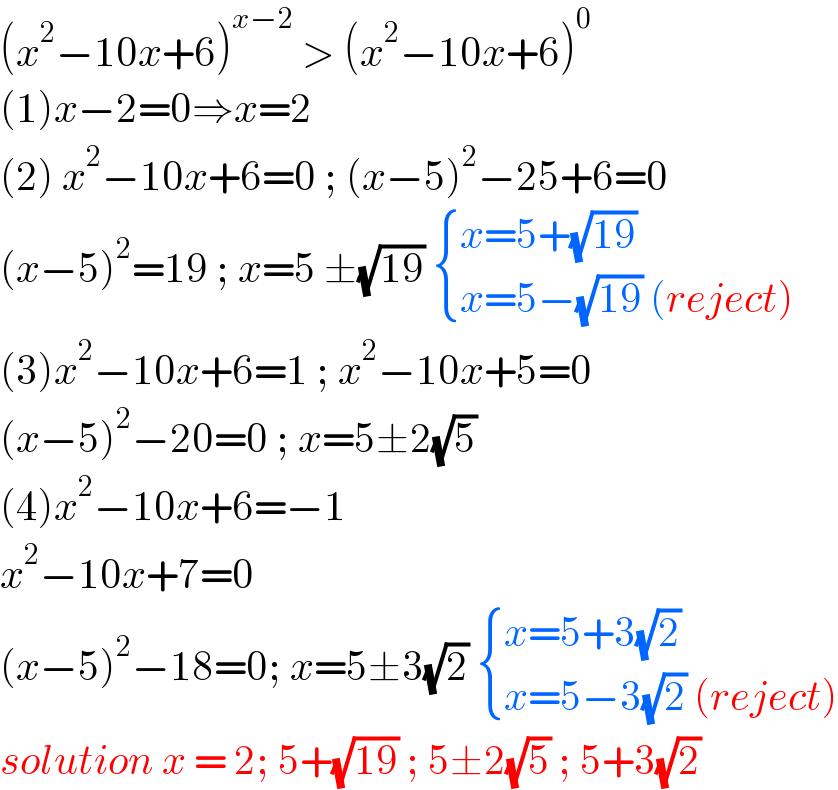
$$\left({x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{6}\right)^{{x}−\mathrm{2}} \:>\:\left({x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{6}\right)^{\mathrm{0}} \\ $$$$\left(\mathrm{1}\right){x}−\mathrm{2}=\mathrm{0}\Rightarrow{x}=\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{6}=\mathrm{0}\:;\:\left({x}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{25}+\mathrm{6}=\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{19}\:;\:{x}=\mathrm{5}\:\pm\sqrt{\mathrm{19}}\:\begin{cases}{{x}=\mathrm{5}+\sqrt{\mathrm{19}}}\\{{x}=\mathrm{5}−\sqrt{\mathrm{19}}\:\left({reject}\right)}\end{cases} \\ $$$$\left(\mathrm{3}\right){x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{6}=\mathrm{1}\:;\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{20}=\mathrm{0}\:;\:{x}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\left(\mathrm{4}\right){x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{6}=−\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{7}=\mathrm{0} \\ $$$$\left({x}−\mathrm{5}\right)^{\mathrm{2}} −\mathrm{18}=\mathrm{0};\:{x}=\mathrm{5}\pm\mathrm{3}\sqrt{\mathrm{2}}\:\begin{cases}{{x}=\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}}}\\{{x}=\mathrm{5}−\mathrm{3}\sqrt{\mathrm{2}}\:\left({reject}\right)}\end{cases} \\ $$$${solution}\:{x}\:=\:\mathrm{2};\:\mathrm{5}+\sqrt{\mathrm{19}}\:;\:\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{5}}\:;\:\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}}\: \\ $$
