Question Number 8762 by tawakalitu last updated on 26/Oct/16
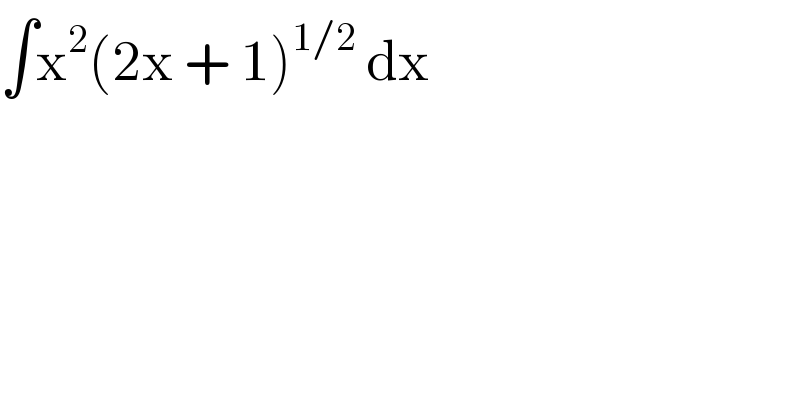
$$\int\mathrm{x}^{\mathrm{2}} \left(\mathrm{2x}\:+\:\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} \:\mathrm{dx} \\ $$
Answered by sou1618 last updated on 26/Oct/16
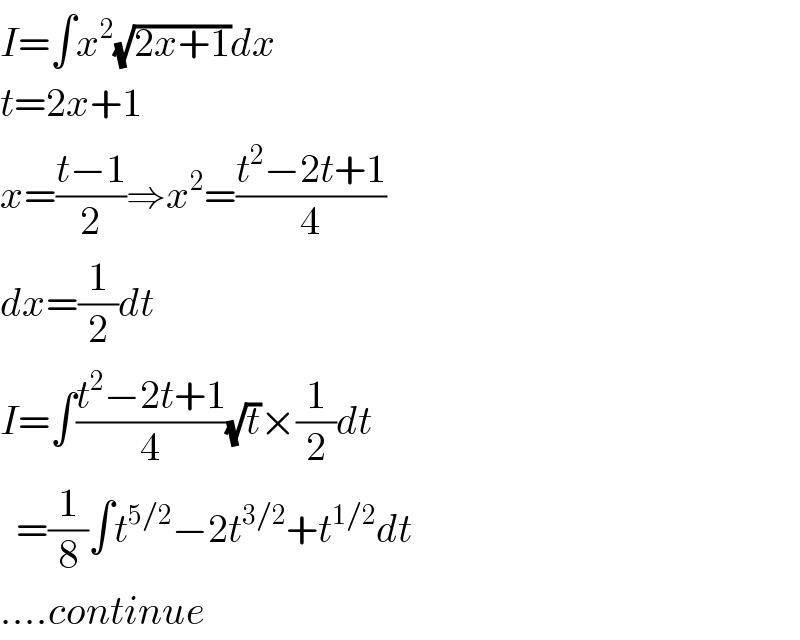
$${I}=\int{x}^{\mathrm{2}} \sqrt{\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$$${t}=\mathrm{2}{x}+\mathrm{1} \\ $$$${x}=\frac{{t}−\mathrm{1}}{\mathrm{2}}\Rightarrow{x}^{\mathrm{2}} =\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{\mathrm{4}} \\ $$$${dx}=\frac{\mathrm{1}}{\mathrm{2}}{dt} \\ $$$${I}=\int\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{\mathrm{4}}\sqrt{{t}}×\frac{\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int{t}^{\mathrm{5}/\mathrm{2}} −\mathrm{2}{t}^{\mathrm{3}/\mathrm{2}} +{t}^{\mathrm{1}/\mathrm{2}} {dt} \\ $$$$….{continue} \\ $$
Commented by tawakalitu last updated on 26/Oct/16
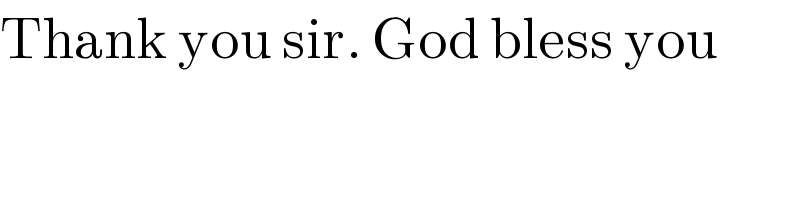
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
