Question Number 202 by 02@>@0 last updated on 25/Jan/15
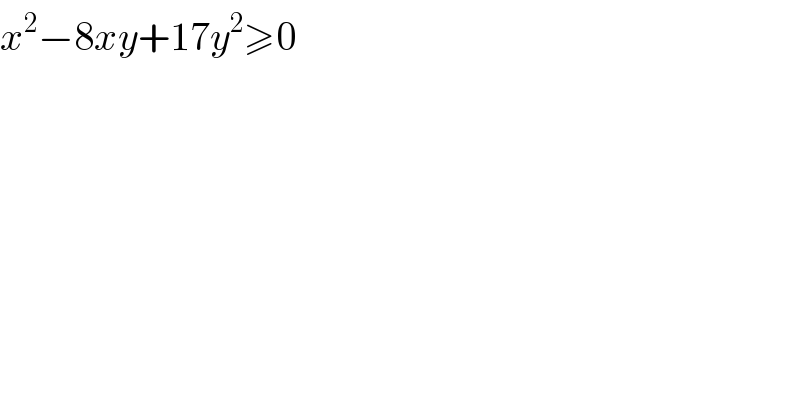
$${x}^{\mathrm{2}} −\mathrm{8}{xy}+\mathrm{17}{y}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$
Answered by prakash jain last updated on 16/Dec/14
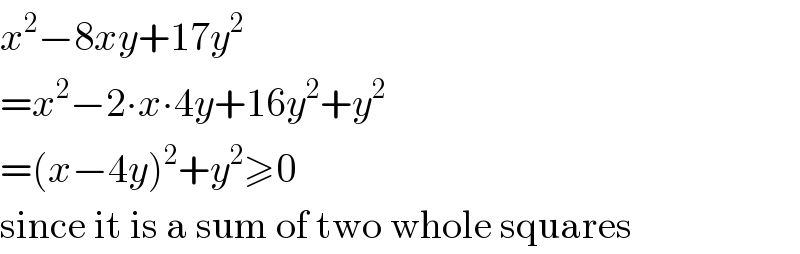
$${x}^{\mathrm{2}} −\mathrm{8}{xy}+\mathrm{17}{y}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}\centerdot{x}\centerdot\mathrm{4}{y}+\mathrm{16}{y}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$=\left({x}−\mathrm{4}{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{two}\:\mathrm{whole}\:\mathrm{squares} \\ $$
