Question Number 12619 by @ANTARES_VY last updated on 27/Apr/17
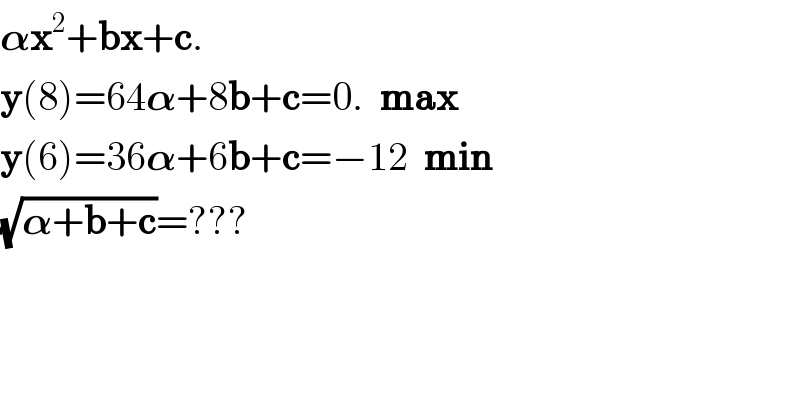
$$\boldsymbol{\alpha\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{bx}}+\boldsymbol{\mathrm{c}}. \\ $$$$\boldsymbol{\mathrm{y}}\left(\mathrm{8}\right)=\mathrm{64}\boldsymbol{\alpha}+\mathrm{8}\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}=\mathrm{0}.\:\:\boldsymbol{\mathrm{max}} \\ $$$$\boldsymbol{\mathrm{y}}\left(\mathrm{6}\right)=\mathrm{36}\boldsymbol{\alpha}+\mathrm{6}\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}=−\mathrm{12}\:\:\boldsymbol{\mathrm{min}} \\ $$$$\sqrt{\boldsymbol{\alpha}+\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{c}}}=??? \\ $$
Commented by prakash jain last updated on 29/Apr/17
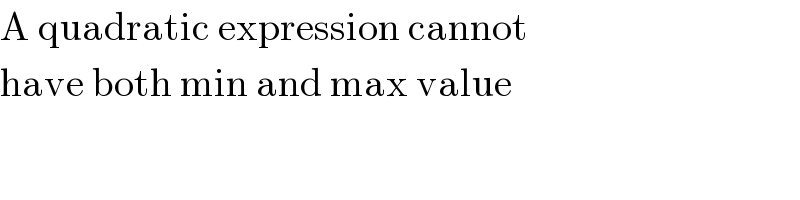
$$\mathrm{A}\:\mathrm{quadratic}\:\mathrm{expression}\:\mathrm{cannot} \\ $$$$\mathrm{have}\:\mathrm{both}\:\mathrm{min}\:\mathrm{and}\:\mathrm{max}\:\mathrm{value} \\ $$
