Question Number 77552 by lémùst last updated on 07/Jan/20
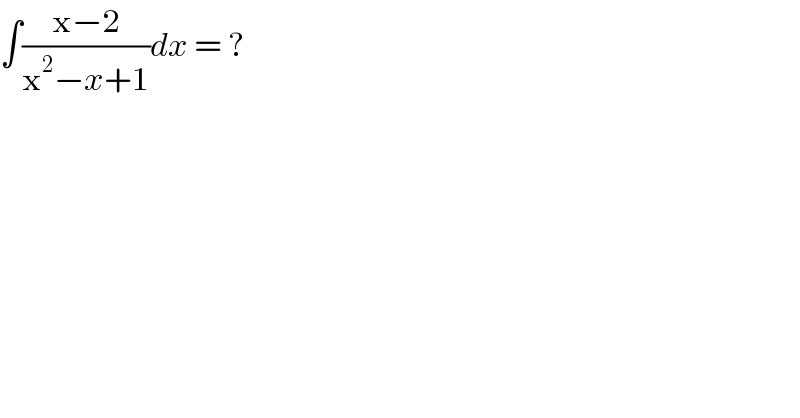
$$\int\frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:=\:? \\ $$
Answered by MJS last updated on 07/Jan/20
![∫((x−2)/(x^2 −x+1))dx=(1/2)∫((2x−4)/(x^2 −x+1))dx= =(1/2)∫((2x−1)/(x^2 −x+1))dx−(3/2)∫(dx/(x^2 −x+1))= (1/2)∫((2x−1)/(x^2 −x+1))dx=(1/2)ln (x^2 −x+1) −(3/2)∫(dx/(x^2 −x+1))=−(3/2)∫(dx/((x−(1/2))^2 +(3/4)))= [t=((√3)/3)(2x−1) → dx=((√3)/2)dt] =−(√3)∫(dt/(t^2 +1))=−(√3)arctan t =−(√3)arctan (((√3)(2x−1))/3) =(1/2)ln (x^2 −x+1) −(√3)arctan (((√3)(2x−1))/3) +C](https://www.tinkutara.com/question/Q77557.png)
$$\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{4}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$ \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}=−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}\right] \\ $$$$\:\:\:\:\:=−\sqrt{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=−\sqrt{\mathrm{3}}\mathrm{arctan}\:{t}\:=−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:−\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:+{C} \\ $$
Commented by lémùst last updated on 07/Jan/20

$$\mathrm{thank}\:\mathrm{you}\:! \\ $$
