Question Number 7798 by Tawakalitu. last updated on 16/Sep/16
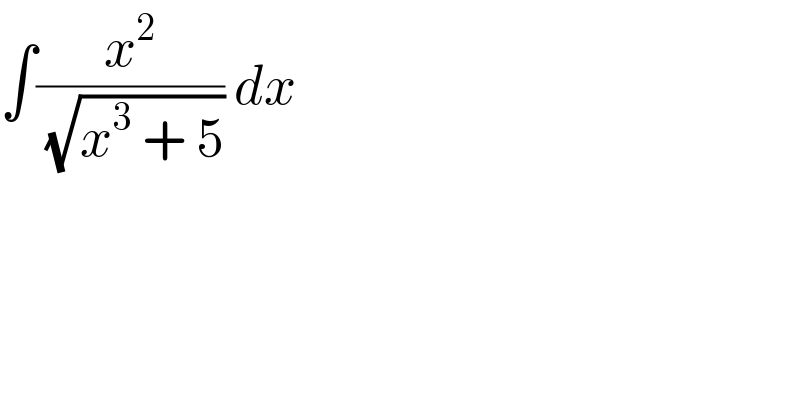
$$\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{3}} \:+\:\mathrm{5}}}\:{dx} \\ $$
Commented by sou1618 last updated on 16/Sep/16
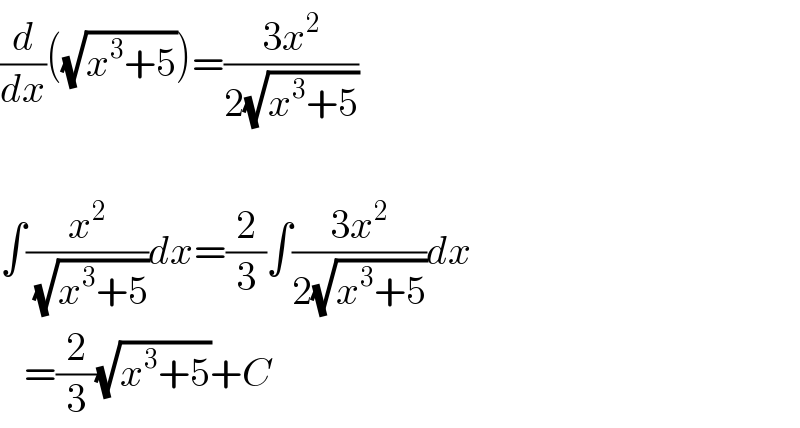
$$\frac{{d}}{{dx}}\left(\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}\right)=\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}} \\ $$$$ \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}}{dx}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}\sqrt{{x}^{\mathrm{3}} +\mathrm{5}}+{C} \\ $$
Commented by Tawakalitu. last updated on 16/Sep/16
$${Wow},\:{thank}\:{you}\:{sir}.\:{i}\:{really}\:{appreciate}. \\ $$
