Question Number 134647 by SOMEDAVONG last updated on 06/Mar/21
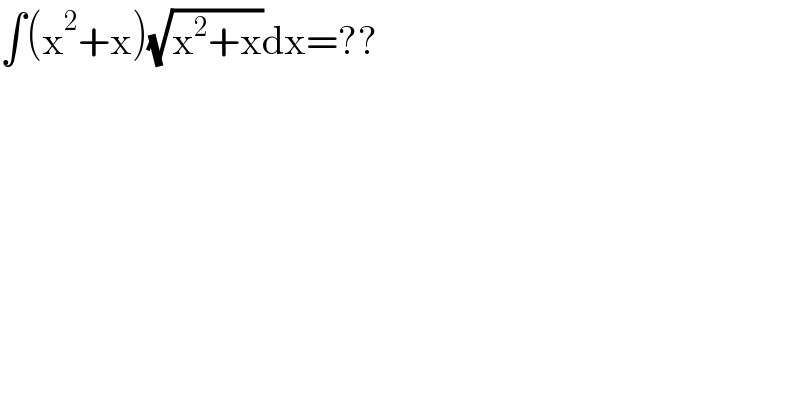
$$\int\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\mathrm{dx}=?? \\ $$
Answered by benjo_mathlover last updated on 06/Mar/21
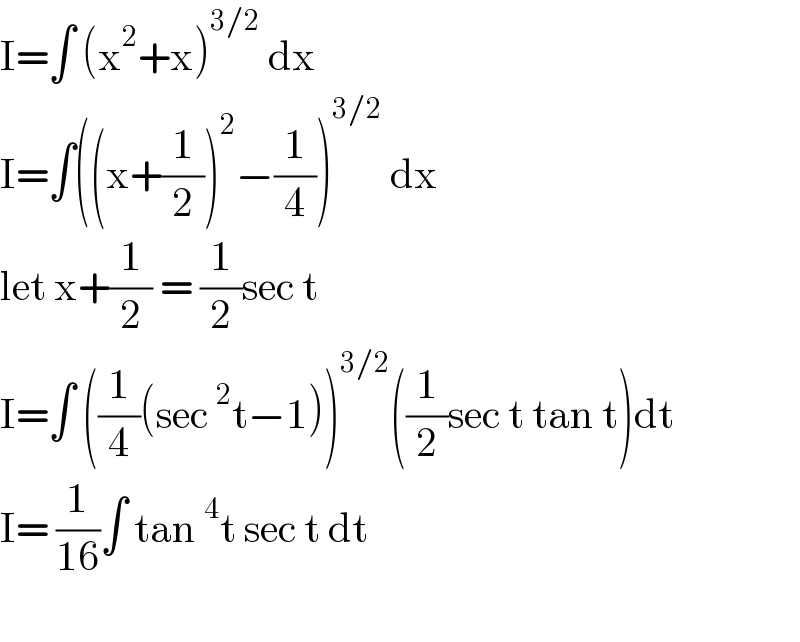
$$\mathrm{I}=\int\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}/\mathrm{2}} \:\mathrm{dx} \\ $$$$\mathrm{I}=\int\left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}/\mathrm{2}} \:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\: \\ $$$$\mathrm{I}=\int\:\left(\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}−\mathrm{1}\right)\right)^{\mathrm{3}/\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:\mathrm{t}\:\mathrm{tan}\:\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{16}}\int\:\mathrm{tan}\:^{\mathrm{4}} \mathrm{t}\:\mathrm{sec}\:\mathrm{t}\:\mathrm{dt}\: \\ $$$$ \\ $$
Answered by Olaf last updated on 06/Mar/21
![Ω = ∫x^(3/2) (x+1)^(3/2) dx Let u = x+(1/2) Ω = ∫(u^2 −(1/4))^(3/2) du Let u = (1/2)chv Ω = ∫((1/4)ch^2 v−(1/4))^(3/2) (1/2)shvdv Ω = (1/8)∫sh^4 vdv Ω = (1/8)∫((ch(4v)−4ch(2v)+3)/8)dv Ω = (1/(64))[(1/4)sh(4v)−(1/2)sh(2v)+3v]+C with v = argch(2u) = argch(2x+1) Now use : sh(4v) = 8sh^3 vchv+4shvchv and sh(2v) = 2shvchv ...](https://www.tinkutara.com/question/Q134654.png)
$$\Omega\:=\:\int{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Omega\:=\:\int\left({u}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {du} \\ $$$$\mathrm{Let}\:{u}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ch}{v} \\ $$$$\Omega\:=\:\int\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ch}^{\mathrm{2}} {v}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}{vdv} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{sh}^{\mathrm{4}} {vdv} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\mathrm{ch}\left(\mathrm{4}{v}\right)−\mathrm{4ch}\left(\mathrm{2}{v}\right)+\mathrm{3}}{\mathrm{8}}{dv} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{64}}\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sh}\left(\mathrm{4}{v}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{2}{v}\right)+\mathrm{3}{v}\right]+\mathrm{C} \\ $$$$\mathrm{with}\:{v}\:=\:\mathrm{argch}\left(\mathrm{2}{u}\right)\:=\:\mathrm{argch}\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\mathrm{Now}\:\mathrm{use}\:: \\ $$$$\mathrm{sh}\left(\mathrm{4}{v}\right)\:=\:\mathrm{8sh}^{\mathrm{3}} {v}\mathrm{ch}{v}+\mathrm{4sh}{v}\mathrm{ch}{v} \\ $$$$\mathrm{and} \\ $$$$\mathrm{sh}\left(\mathrm{2}{v}\right)\:=\:\mathrm{2sh}{v}\mathrm{ch}{v} \\ $$$$… \\ $$
Answered by mathmax by abdo last updated on 07/Mar/21
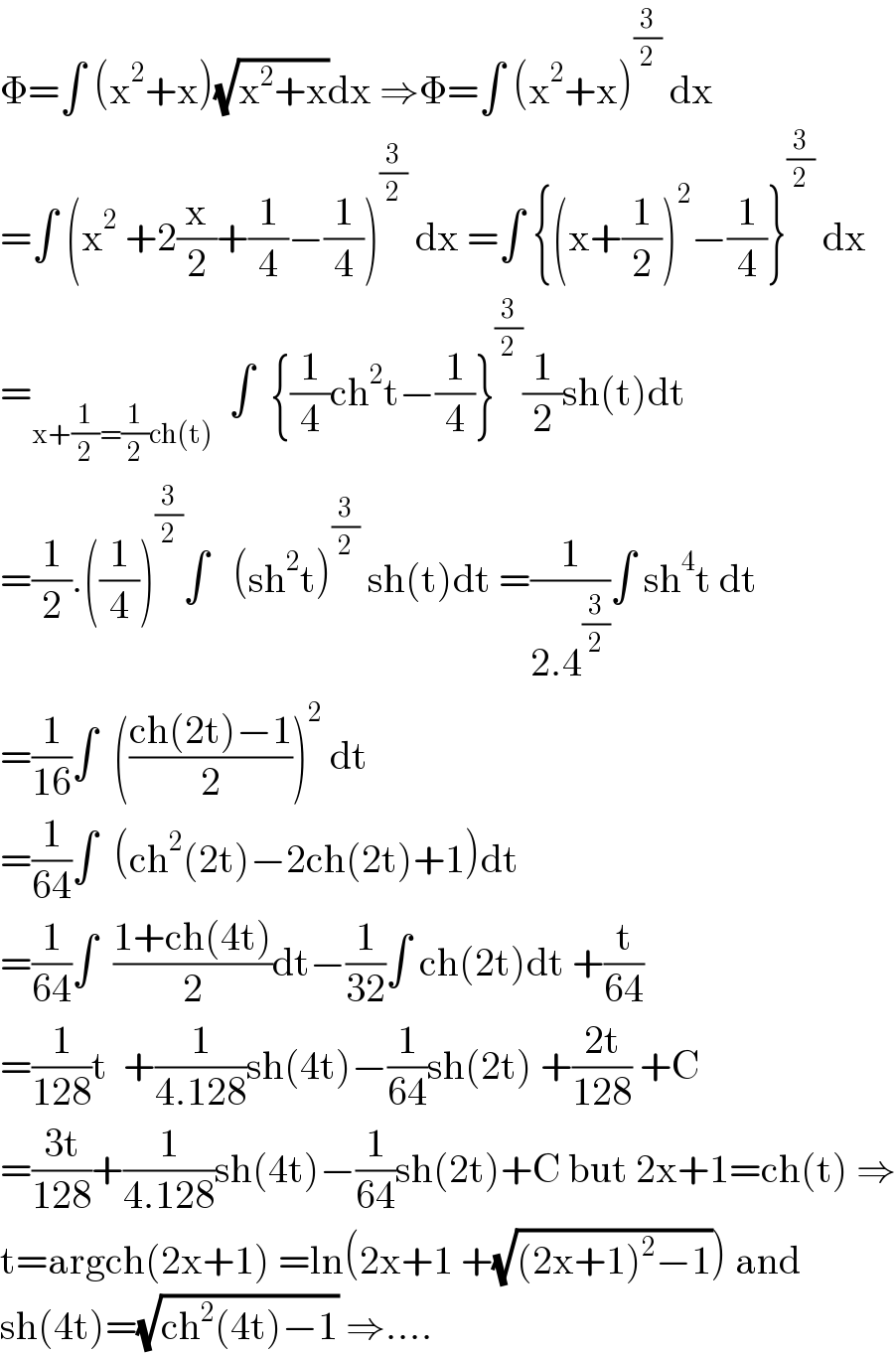
$$\Phi=\int\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\mathrm{dx}\:\Rightarrow\Phi=\int\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$=\int\:\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx}\:=\int\:\left\{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$=_{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ch}\left(\mathrm{t}\right)} \:\:\int\:\:\left\{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ch}^{\mathrm{2}} \mathrm{t}−\frac{\mathrm{1}}{\mathrm{4}}\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \int\:\:\:\left(\mathrm{sh}^{\mathrm{2}} \mathrm{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} }\int\:\mathrm{sh}^{\mathrm{4}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\int\:\:\left(\frac{\mathrm{ch}\left(\mathrm{2t}\right)−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\:\left(\mathrm{ch}^{\mathrm{2}} \left(\mathrm{2t}\right)−\mathrm{2ch}\left(\mathrm{2t}\right)+\mathrm{1}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\int\:\:\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{4t}\right)}{\mathrm{2}}\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{32}}\int\:\mathrm{ch}\left(\mathrm{2t}\right)\mathrm{dt}\:+\frac{\mathrm{t}}{\mathrm{64}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{128}}\mathrm{t}\:\:+\frac{\mathrm{1}}{\mathrm{4}.\mathrm{128}}\mathrm{sh}\left(\mathrm{4t}\right)−\frac{\mathrm{1}}{\mathrm{64}}\mathrm{sh}\left(\mathrm{2t}\right)\:+\frac{\mathrm{2t}}{\mathrm{128}}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{3t}}{\mathrm{128}}+\frac{\mathrm{1}}{\mathrm{4}.\mathrm{128}}\mathrm{sh}\left(\mathrm{4t}\right)−\frac{\mathrm{1}}{\mathrm{64}}\mathrm{sh}\left(\mathrm{2t}\right)+\mathrm{C}\:\mathrm{but}\:\mathrm{2x}+\mathrm{1}=\mathrm{ch}\left(\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{t}=\mathrm{argch}\left(\mathrm{2x}+\mathrm{1}\right)\:=\mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\:+\sqrt{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)\:\mathrm{and} \\ $$$$\mathrm{sh}\left(\mathrm{4t}\right)=\sqrt{\mathrm{ch}^{\mathrm{2}} \left(\mathrm{4t}\right)−\mathrm{1}}\:\Rightarrow…. \\ $$
