Question Number 143584 by Huy last updated on 16/Jun/21
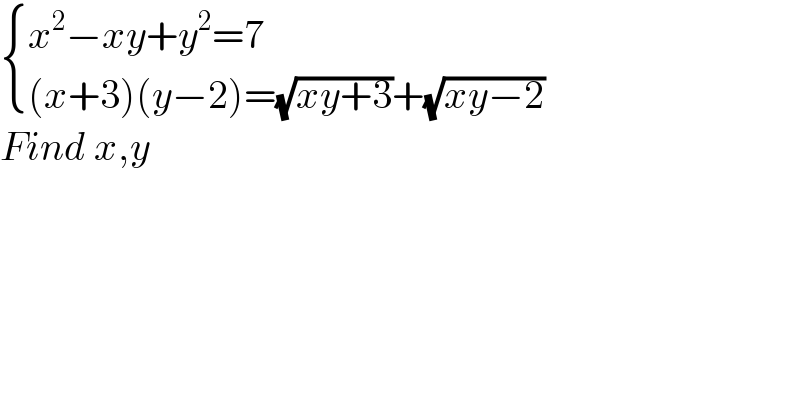
$$\begin{cases}{{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7}}\\{\left({x}+\mathrm{3}\right)\left({y}−\mathrm{2}\right)=\sqrt{{xy}+\mathrm{3}}+\sqrt{{xy}−\mathrm{2}}}\end{cases} \\ $$$${Find}\:{x},{y} \\ $$
Answered by MJS_new last updated on 16/Jun/21
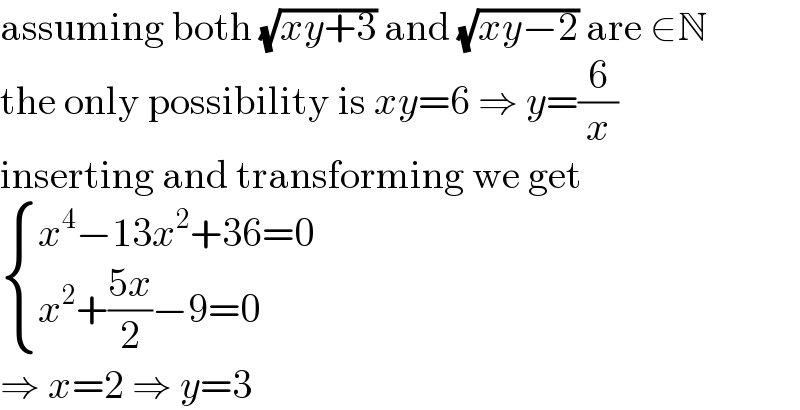
$$\mathrm{assuming}\:\mathrm{both}\:\sqrt{{xy}+\mathrm{3}}\:\mathrm{and}\:\sqrt{{xy}−\mathrm{2}}\:\mathrm{are}\:\in\mathbb{N} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{possibility}\:\mathrm{is}\:{xy}=\mathrm{6}\:\Rightarrow\:{y}=\frac{\mathrm{6}}{{x}} \\ $$$$\mathrm{inserting}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{we}\:\mathrm{get} \\ $$$$\begin{cases}{{x}^{\mathrm{4}} −\mathrm{13}{x}^{\mathrm{2}} +\mathrm{36}=\mathrm{0}}\\{{x}^{\mathrm{2}} +\frac{\mathrm{5}{x}}{\mathrm{2}}−\mathrm{9}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\:{x}=\mathrm{2}\:\Rightarrow\:{y}=\mathrm{3} \\ $$
