Question Number 826 by 123456 last updated on 18/Mar/15
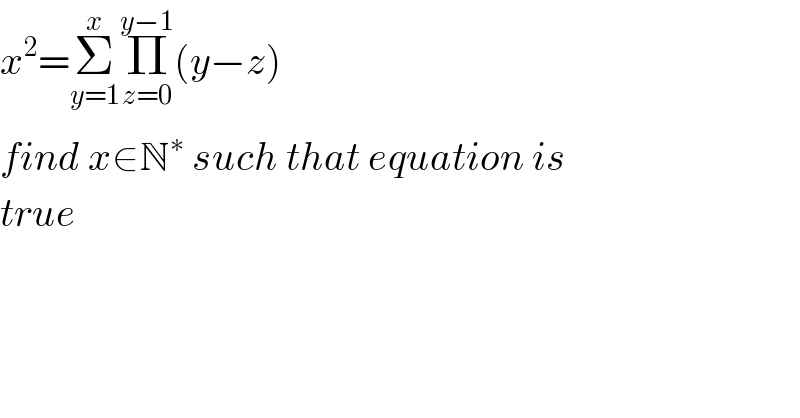
$${x}^{\mathrm{2}} =\underset{{y}=\mathrm{1}} {\overset{{x}} {\sum}}\underset{{z}=\mathrm{0}} {\overset{{y}−\mathrm{1}} {\prod}}\left({y}−{z}\right) \\ $$$${find}\:{x}\in\mathbb{N}^{\ast} \:{such}\:{that}\:{equation}\:{is} \\ $$$${true} \\ $$
Commented by 123456 last updated on 18/Mar/15
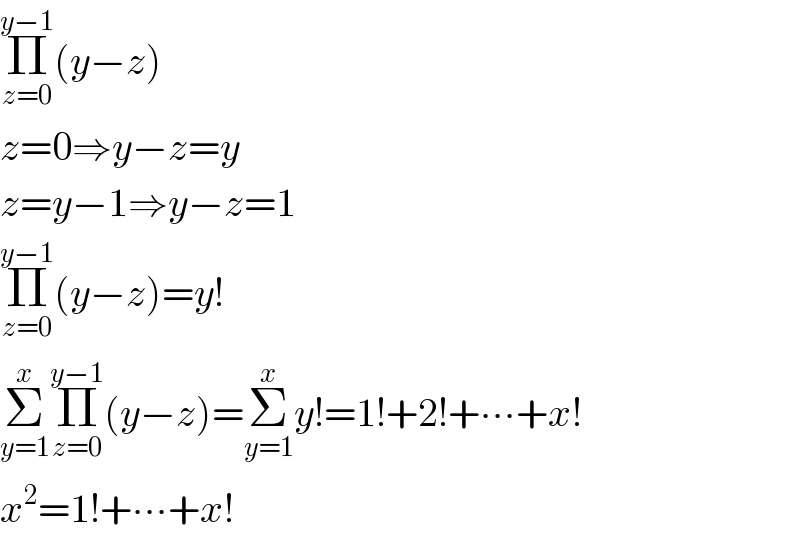
$$\underset{{z}=\mathrm{0}} {\overset{{y}−\mathrm{1}} {\prod}}\left({y}−{z}\right) \\ $$$${z}=\mathrm{0}\Rightarrow{y}−{z}={y} \\ $$$${z}={y}−\mathrm{1}\Rightarrow{y}−{z}=\mathrm{1} \\ $$$$\underset{{z}=\mathrm{0}} {\overset{{y}−\mathrm{1}} {\prod}}\left({y}−{z}\right)={y}! \\ $$$$\underset{{y}=\mathrm{1}} {\overset{{x}} {\sum}}\underset{{z}=\mathrm{0}} {\overset{{y}−\mathrm{1}} {\prod}}\left({y}−{z}\right)=\underset{{y}=\mathrm{1}} {\overset{{x}} {\sum}}{y}!=\mathrm{1}!+\mathrm{2}!+\centerdot\centerdot\centerdot+{x}! \\ $$$${x}^{\mathrm{2}} =\mathrm{1}!+\centerdot\centerdot\centerdot+{x}! \\ $$
Answered by prakash jain last updated on 18/Mar/15

$${x}=\mathrm{3}\:\mathrm{and}\:\:{x}=\mathrm{1}\:\mathrm{are}\:\mathrm{solutions}. \\ $$$${x}!>{x}^{\mathrm{2}} \:\:\mathrm{for}\:{x}\geqslant\mathrm{4} \\ $$$${x}=\mathrm{4}\:,\:{x}!=\mathrm{24},\:{x}^{\mathrm{2}} =\mathrm{16},\:\:{x}!>{x}^{\mathrm{2}} \\ $$$$\mathrm{If}\:{x}!>{x}^{\mathrm{2}} \:\mathrm{then}\:\mathrm{for}\:{x}>\mathrm{4} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)!={x}!\left({x}+\mathrm{1}\right)>{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)={x}^{\mathrm{2}} +{x}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +{x}^{\mathrm{3}} −\mathrm{1}+\mathrm{1}={x}^{\mathrm{2}} +\mathrm{1}+\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:>{x}^{\mathrm{2}} +\mathrm{1}+{x}^{\mathrm{2}} +{x}+\mathrm{1}\:>{x}^{\mathrm{2}} +\mathrm{1}+{x}+{x}+\mathrm{1}\:\because{x}^{\mathrm{2}} >{x}\:\wedge{x}>\mathrm{1} \\ $$$$\:\:\:\:\:\:\:>\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}>\left({x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{x}\geqslant\mathrm{4}. \\ $$
