Question Number 72175 by mr W last updated on 26/Oct/19
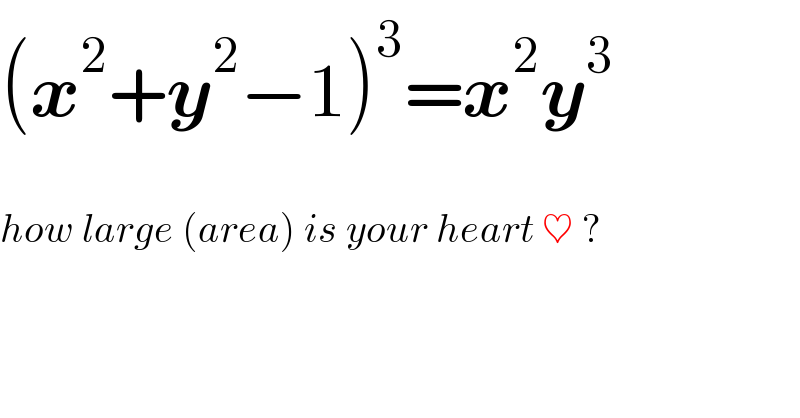
$$\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} =\boldsymbol{{x}}^{\mathrm{2}} \boldsymbol{{y}}^{\mathrm{3}} \\ $$$$ \\ $$$${how}\:{large}\:\left({area}\right)\:{is}\:{your}\:{heart}\:\heartsuit\:? \\ $$
Commented by mr W last updated on 26/Oct/19
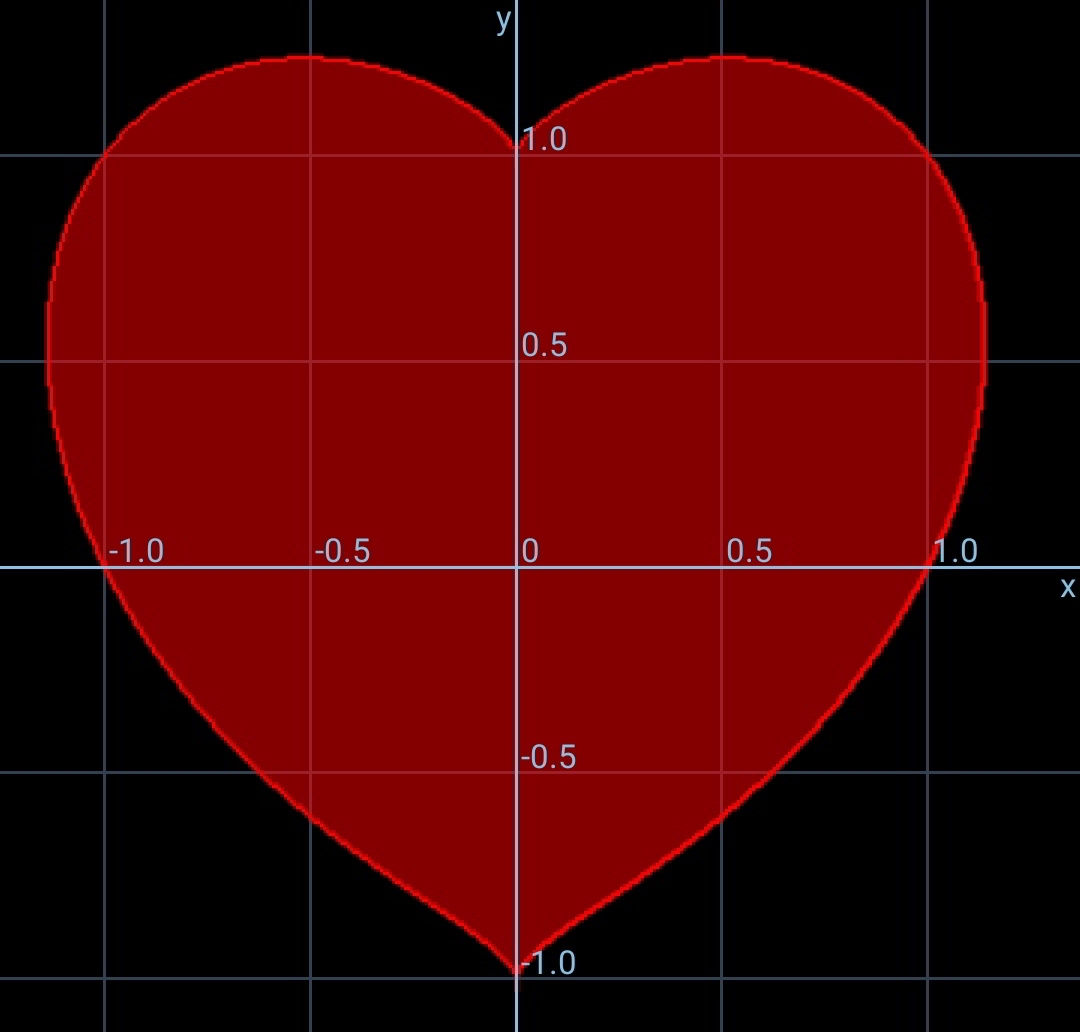
Commented by MJS last updated on 26/Oct/19

$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{for}\:{x};\:\mathrm{we}\:\mathrm{get}\:\mathrm{3}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{6}\:\mathrm{solutions}\:\pm\sqrt{{x}^{\mathrm{2}} }\:\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{exact} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{border}\:\mathrm{is}\:\mathrm{a}\:\mathrm{problem} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{also}\:\mathrm{tried}\:\mathrm{polar}\:\mathrm{coordinates}\:\mathrm{but}\:\mathrm{cannot}\:\mathrm{solve} \\ $$$$\mathrm{for}\:{r} \\ $$
Commented by mr W last updated on 26/Oct/19

$${thanks}\:{sir}!\:{it}\:{seems}\:{to}\:{be}\:{impossible}\:{to} \\ $$$${get}\:{the}\:{exact}\:{value}\:{of}\:{the}\:{area}. \\ $$
Answered by ajfour last updated on 26/Oct/19
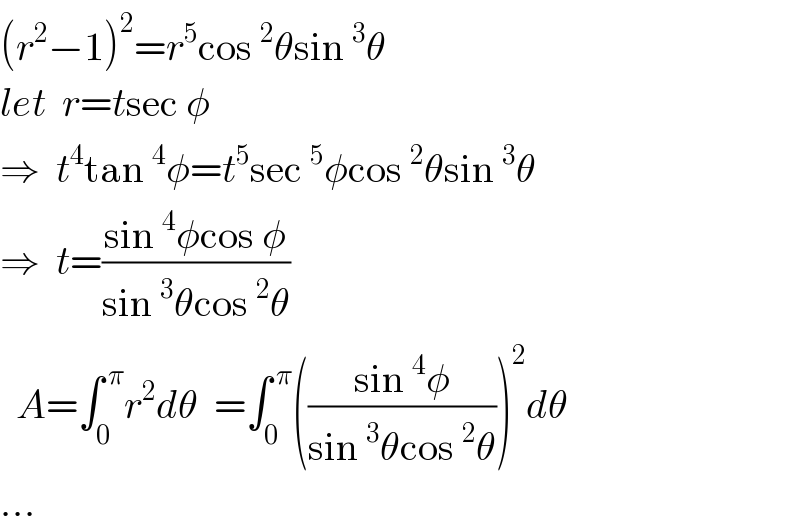
$$\left({r}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={r}^{\mathrm{5}} \mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:^{\mathrm{3}} \theta \\ $$$${let}\:\:{r}={t}\mathrm{sec}\:\phi \\ $$$$\Rightarrow\:\:{t}^{\mathrm{4}} \mathrm{tan}\:^{\mathrm{4}} \phi={t}^{\mathrm{5}} \mathrm{sec}\:^{\mathrm{5}} \phi\mathrm{cos}\:^{\mathrm{2}} \theta\mathrm{sin}\:^{\mathrm{3}} \theta \\ $$$$\Rightarrow\:\:{t}=\frac{\mathrm{sin}\:^{\mathrm{4}} \phi\mathrm{cos}\:\phi}{\mathrm{sin}\:^{\mathrm{3}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta} \\ $$$$\:\:{A}=\int_{\mathrm{0}} ^{\:\pi} {r}^{\mathrm{2}} {d}\theta\:\:=\int_{\mathrm{0}} ^{\:\pi} \left(\frac{\mathrm{sin}\:^{\mathrm{4}} \phi}{\mathrm{sin}\:^{\mathrm{3}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta}\right)^{\mathrm{2}} {d}\theta \\ $$$$… \\ $$
