Question Number 142556 by iloveisrael last updated on 02/Jun/21

$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}{yz}+\mathrm{2}−{z}^{\mathrm{2}} }\\{{z}=\mathrm{4022}−{x}−{y}}\end{cases} \\ $$$$\:{x},{y},{z}\in\mathbb{Z}^{+} \:.\:{then}\:{z}= \\ $$
Answered by iloveisrael last updated on 02/Jun/21
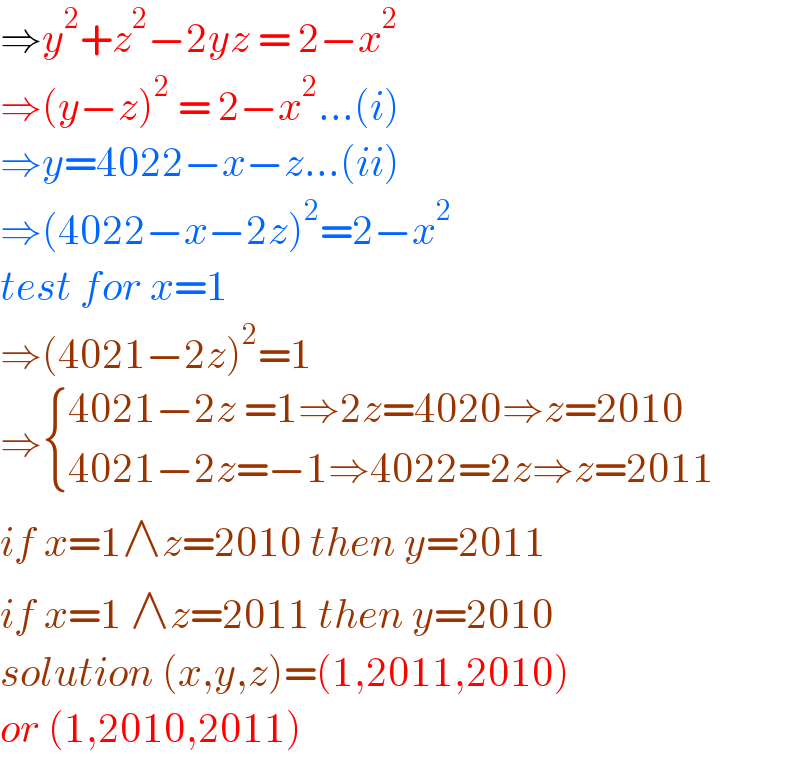
$$\Rightarrow{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{yz}\:=\:\mathrm{2}−{x}^{\mathrm{2}} \\ $$$$\Rightarrow\left({y}−{z}\right)^{\mathrm{2}} \:=\:\mathrm{2}−{x}^{\mathrm{2}} …\left({i}\right) \\ $$$$\Rightarrow{y}=\mathrm{4022}−{x}−{z}…\left({ii}\right) \\ $$$$\Rightarrow\left(\mathrm{4022}−{x}−\mathrm{2}{z}\right)^{\mathrm{2}} =\mathrm{2}−{x}^{\mathrm{2}} \\ $$$${test}\:{for}\:{x}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{4021}−\mathrm{2}{z}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\begin{cases}{\mathrm{4021}−\mathrm{2}{z}\:=\mathrm{1}\Rightarrow\mathrm{2}{z}=\mathrm{4020}\Rightarrow{z}=\mathrm{2010}}\\{\mathrm{4021}−\mathrm{2}{z}=−\mathrm{1}\Rightarrow\mathrm{4022}=\mathrm{2}{z}\Rightarrow{z}=\mathrm{2011}}\end{cases} \\ $$$${if}\:{x}=\mathrm{1}\wedge{z}=\mathrm{2010}\:{then}\:{y}=\mathrm{2011} \\ $$$${if}\:{x}=\mathrm{1}\:\wedge{z}=\mathrm{2011}\:{then}\:{y}=\mathrm{2010} \\ $$$${solution}\:\left({x},{y},{z}\right)=\left(\mathrm{1},\mathrm{2011},\mathrm{2010}\right) \\ $$$${or}\:\left(\mathrm{1},\mathrm{2010},\mathrm{2011}\right)\: \\ $$
