Question Number 143832 by mathdanisur last updated on 18/Jun/21
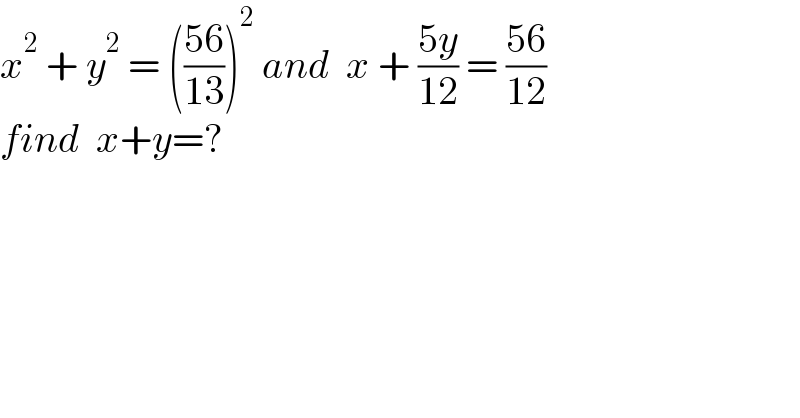
$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:=\:\left(\frac{\mathrm{56}}{\mathrm{13}}\right)^{\mathrm{2}} \:{and}\:\:{x}\:+\:\frac{\mathrm{5}{y}}{\mathrm{12}}\:=\:\frac{\mathrm{56}}{\mathrm{12}} \\ $$$${find}\:\:{x}+{y}=? \\ $$
Answered by MJS_new last updated on 18/Jun/21
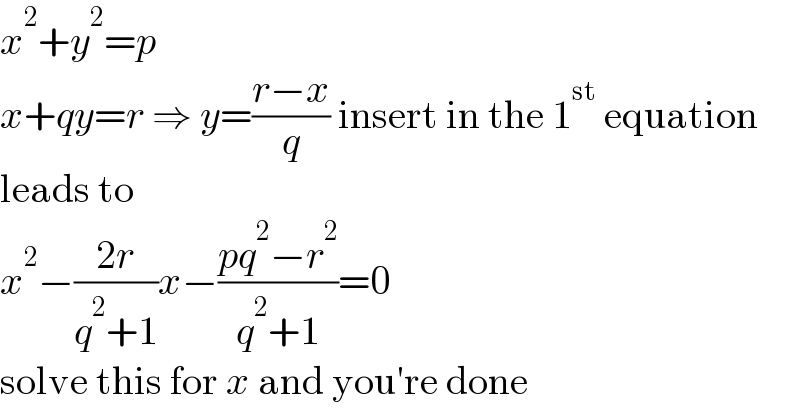
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={p} \\ $$$${x}+{qy}={r}\:\Rightarrow\:{y}=\frac{{r}−{x}}{{q}}\:\mathrm{insert}\:\mathrm{in}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{equation} \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{2}{r}}{{q}^{\mathrm{2}} +\mathrm{1}}{x}−\frac{{pq}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{q}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{for}\:{x}\:\mathrm{and}\:\mathrm{you}'\mathrm{re}\:\mathrm{done} \\ $$
Commented by mathdanisur last updated on 19/Jun/21

$${thanks}\:{Sir}.. \\ $$
Answered by mitica last updated on 18/Jun/21
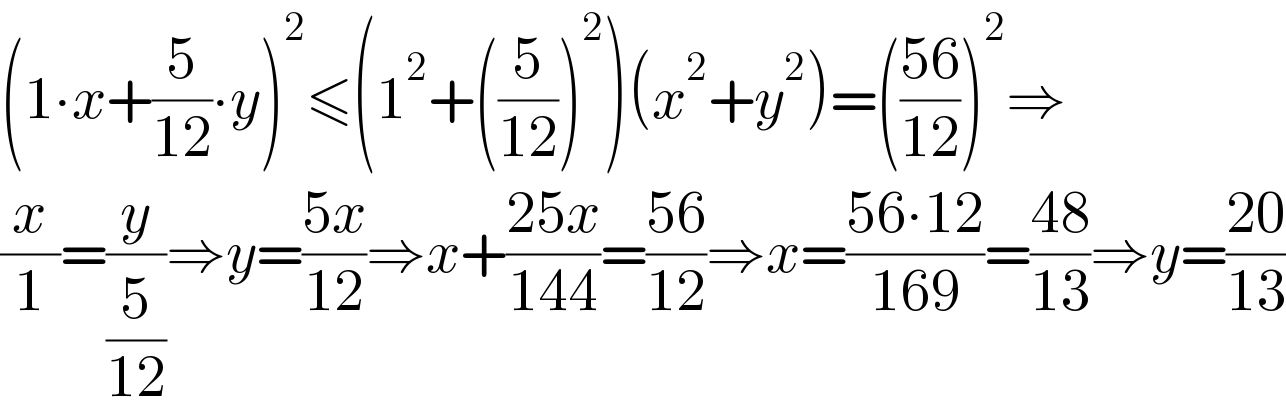
$$\left(\mathrm{1}\centerdot{x}+\frac{\mathrm{5}}{\mathrm{12}}\centerdot{y}\right)^{\mathrm{2}} \leqslant\left(\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{12}}\right)^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\left(\frac{\mathrm{56}}{\mathrm{12}}\right)^{\mathrm{2}} \Rightarrow \\ $$$$\frac{{x}}{\mathrm{1}}=\frac{{y}}{\frac{\mathrm{5}}{\mathrm{12}}}\Rightarrow{y}=\frac{\mathrm{5}{x}}{\mathrm{12}}\Rightarrow{x}+\frac{\mathrm{25}{x}}{\mathrm{144}}=\frac{\mathrm{56}}{\mathrm{12}}\Rightarrow{x}=\frac{\mathrm{56}\centerdot\mathrm{12}}{\mathrm{169}}=\frac{\mathrm{48}}{\mathrm{13}}\Rightarrow{y}=\frac{\mathrm{20}}{\mathrm{13}} \\ $$
Commented by mathdanisur last updated on 19/Jun/21
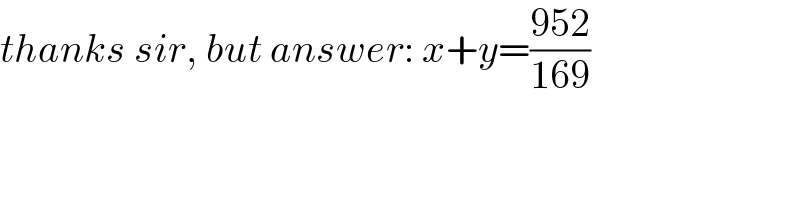
$${thanks}\:{sir},\:{but}\:{answer}:\:{x}+{y}=\frac{\mathrm{952}}{\mathrm{169}} \\ $$
Answered by mr W last updated on 19/Jun/21
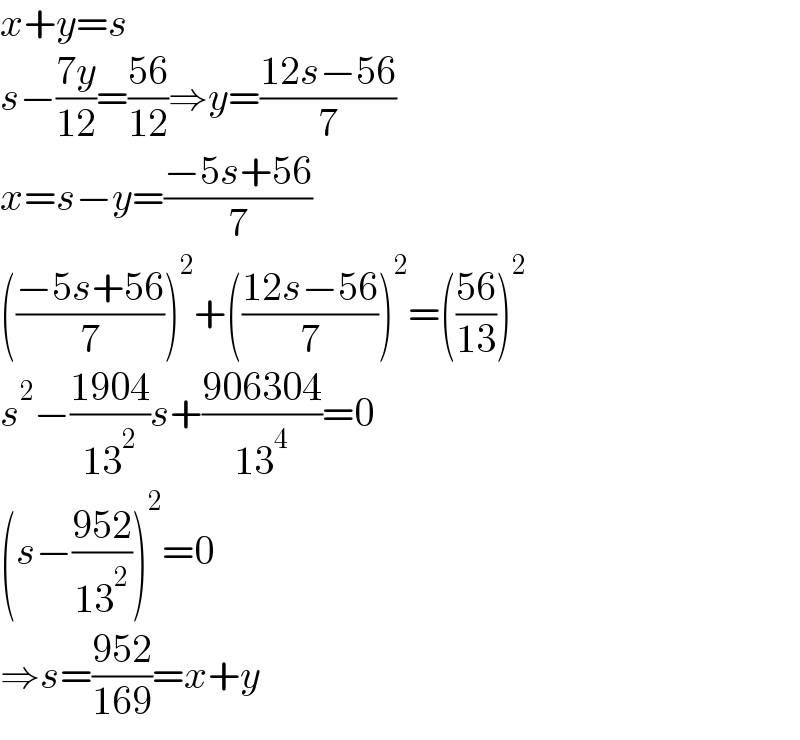
$${x}+{y}={s} \\ $$$${s}−\frac{\mathrm{7}{y}}{\mathrm{12}}=\frac{\mathrm{56}}{\mathrm{12}}\Rightarrow{y}=\frac{\mathrm{12}{s}−\mathrm{56}}{\mathrm{7}} \\ $$$${x}={s}−{y}=\frac{−\mathrm{5}{s}+\mathrm{56}}{\mathrm{7}} \\ $$$$\left(\frac{−\mathrm{5}{s}+\mathrm{56}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{12}{s}−\mathrm{56}}{\mathrm{7}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{56}}{\mathrm{13}}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} −\frac{\mathrm{1904}}{\mathrm{13}^{\mathrm{2}} }{s}+\frac{\mathrm{906304}}{\mathrm{13}^{\mathrm{4}} }=\mathrm{0} \\ $$$$\left({s}−\frac{\mathrm{952}}{\mathrm{13}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}=\frac{\mathrm{952}}{\mathrm{169}}={x}+{y} \\ $$
Commented by mathdanisur last updated on 19/Jun/21
$${cool}\:{dear}\:{Sir}\:{thank}\:{you}.. \\ $$
