Question Number 73399 by mathocean1 last updated on 11/Nov/19
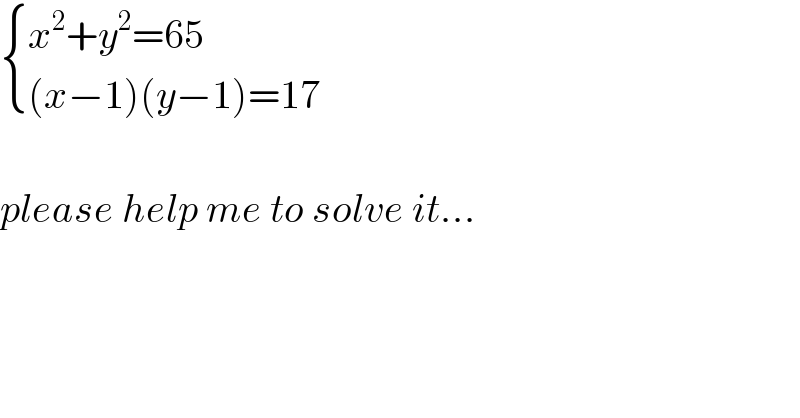
$$\begin{cases}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{65}}\\{\left({x}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)=\mathrm{17}}\end{cases} \\ $$$$ \\ $$$${please}\:{help}\:{me}\:{to}\:{solve}\:{it}… \\ $$
Commented by abdomathmax last updated on 11/Nov/19

$$\Rightarrow\begin{cases}{\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\:=\mathrm{65}}\\{{xy}−\left({x}+{y}\right)+\mathrm{1}\:=\mathrm{17}\:\Rightarrow\begin{cases}{{s}^{\mathrm{2}} −\mathrm{2}{p}\:=\mathrm{65}}\\{{p}−{s}\:=\mathrm{16}\:\Rightarrow}\end{cases}}\end{cases} \\ $$$$\begin{cases}{{s}^{\mathrm{2}} −\mathrm{2}{p}=\mathrm{65}}\\{\mathrm{2}{p}=\mathrm{2}{s}+\mathrm{32}\:\Rightarrow\begin{cases}{{s}^{\mathrm{2}} −\left(\mathrm{2}{s}+\mathrm{32}\right)=\mathrm{65}}\\{{p}={s}+\mathrm{16}\:\Rightarrow}\end{cases}}\end{cases} \\ $$$$\begin{cases}{{s}^{\mathrm{2}} −\mathrm{2}{s}\:−\mathrm{32}−\mathrm{65}\:=\mathrm{0}}\\{{p}={s}+\mathrm{16}\:\Rightarrow\begin{cases}{{s}^{\mathrm{2}} −\mathrm{2}{s}\:−\mathrm{97}=\mathrm{0}}\\{{p}={s}+\mathrm{16}\:}\end{cases}}\end{cases} \\ $$$${let}\:{solve}\:\:{s}^{\mathrm{2}} −\mathrm{2}{s}\:−\mathrm{97}\:=\mathrm{0} \\ $$$$\Delta^{'} =\mathrm{98}\:\Rightarrow{s}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{98}}\:{and}\:{s}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{98}} \\ $$$${s}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{98}}\:\Rightarrow{p}_{\mathrm{1}} =\mathrm{17}+\sqrt{\mathrm{98}} \\ $$$${s}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{98}}\:\Rightarrow{p}_{\mathrm{2}} =\mathrm{17}−\sqrt{\mathrm{98}} \\ $$$${we}\:{have}\:{x}+{y}={s}\:{and}\:{xy}={p}\:\Rightarrow{xand}\:{y}\:{are}\:{solution}?{of} \\ $$$${the}\:{equation}\:{X}^{\mathrm{2}} −{sX}\:+{p}\:=\mathrm{0} \\ $$$${s}={s}_{\mathrm{1}} \Rightarrow{X}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{98}}\right){X}\:+\mathrm{17}+\sqrt{\mathrm{98}}=\mathrm{0} \\ $$$$\Delta\:=\left(\mathrm{1}+\sqrt{\mathrm{98}}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{17}+\sqrt{\mathrm{98}}\right)\:=\mathrm{99}\:+\mathrm{2}\sqrt{\mathrm{98}}−\mathrm{68}\:−\mathrm{4}\sqrt{\mathrm{98}} \\ $$$$=\mathrm{31}−\mathrm{2}\sqrt{\mathrm{98}} \\ $$$${x}=\frac{\mathrm{1}+\sqrt{\mathrm{98}}\:+\sqrt{\mathrm{31}−\mathrm{2}\sqrt{\mathrm{98}}}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}+\sqrt{\mathrm{98}}−\sqrt{\mathrm{31}−\mathrm{2}\sqrt{\mathrm{98}}}}{\mathrm{2}} \\ $$$${s}={s}_{\mathrm{2}} \Rightarrow{X}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{98}}\right){X}\:+\left(\mathrm{17}−\sqrt{\mathrm{98}}\right)=\mathrm{0} \\ $$$${and}\:{we}\:{follow}\:{the}\:{same}\:{way}… \\ $$
Answered by $@ty@m123 last updated on 12/Nov/19

$$\left({x}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)=\mathrm{17} \\ $$$${xy}−{x}−{y}+\mathrm{1}=\mathrm{17} \\ $$$$\mathrm{2}{xy}−\mathrm{2}\left({x}+{y}\right)=\mathrm{32}\:….\left(\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{65}\:…\left(\mathrm{2}\right) \\ $$$${Add}\:{ing} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}−\mathrm{2}\left({x}+{y}\right)=\mathrm{97} \\ $$$${k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{97}=\mathrm{0}\:{where}\:{k}={x}+{y} \\ $$$${k}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{388}}}{\mathrm{2}} \\ $$$${k}=\frac{\mathrm{2}\pm\sqrt{\mathrm{392}}}{\mathrm{2}} \\ $$$${k}=\frac{\mathrm{2}\pm\mathrm{19}.\mathrm{8}}{\mathrm{2}} \\ $$$${k}=\frac{\mathrm{21}.\mathrm{8}}{\mathrm{2}},\:\frac{−\mathrm{17}.\mathrm{8}}{\mathrm{2}} \\ $$$${k}=\mathrm{10}.\mathrm{9},\:−\mathrm{8}.\mathrm{9}\:….\left(\mathrm{3}\right) \\ $$$${Subtracting}\:\left(\mathrm{1}\right)\:{from}\:\left(\mathrm{2}\right), \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}+\mathrm{2}\left({x}+{y}\right)=\mathrm{33} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{2}\left({x}+{y}\right)=\mathrm{33}\:…..\left(\mathrm{4}\right) \\ $$$${Case}\:\left({i}\right)\:{k}=\mathrm{10}.\mathrm{9}\:{or}\:{x}+{y}=\mathrm{10}.\mathrm{9}\:…\left(\mathrm{5}\right) \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{21}.\mathrm{8}=\mathrm{33} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{11}.\mathrm{2}\:\Rightarrow\:{x}−{y}=\sqrt{\mathrm{11}.\mathrm{2}}\:\:\:….\left(\mathrm{6}\right) \\ $$$${Now}\:{solve}\:\left(\mathrm{5}\right)\:{and}\:\left(\mathrm{6}\right) \\ $$$$ \\ $$$${Case}\:\left({ii}\right)\:{k}=−\mathrm{8}.\mathrm{9}\:{or}\:{x}+{y}=−\mathrm{8}.\mathrm{9}\:…\left(\mathrm{7}\right) \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} −\mathrm{17}.\mathrm{8}=\mathrm{15} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{17}.\mathrm{8}+\mathrm{15} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{32}.\mathrm{8} \\ $$$${x}−{y}=\sqrt{\mathrm{32}.\mathrm{8}}\:\:…\left(\mathrm{8}\right) \\ $$$${Now}\:{solve}\:\left(\mathrm{7}\right)\:{and}\:\left(\mathrm{8}\right) \\ $$
Answered by ajfour last updated on 11/Nov/19
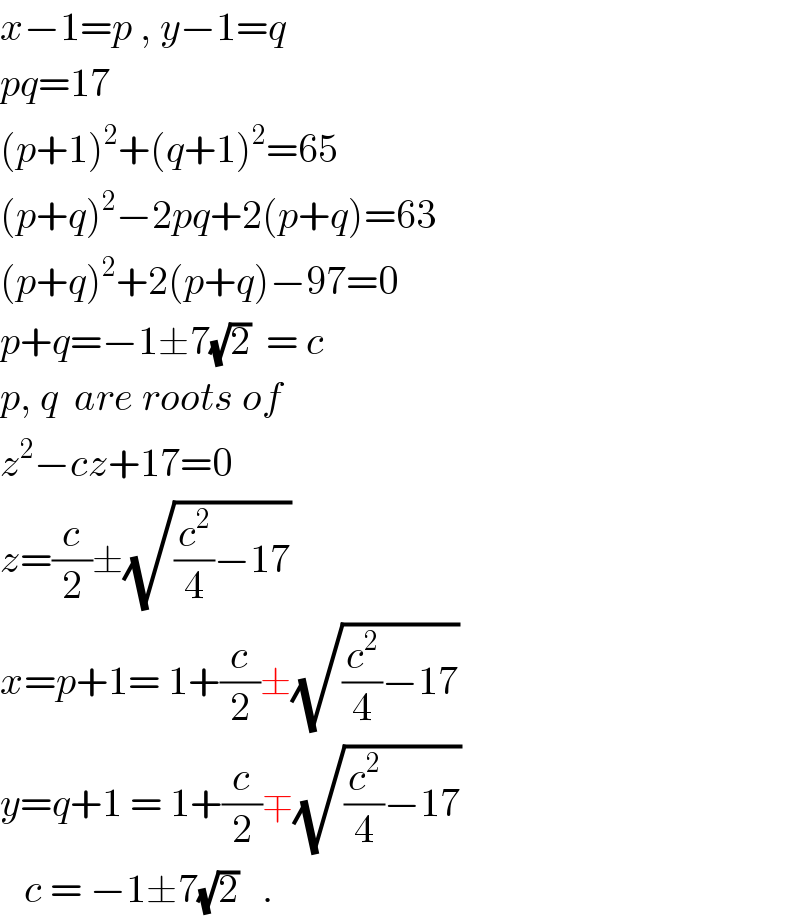
$${x}−\mathrm{1}={p}\:,\:{y}−\mathrm{1}={q} \\ $$$${pq}=\mathrm{17} \\ $$$$\left({p}+\mathrm{1}\right)^{\mathrm{2}} +\left({q}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{65} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq}+\mathrm{2}\left({p}+{q}\right)=\mathrm{63} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} +\mathrm{2}\left({p}+{q}\right)−\mathrm{97}=\mathrm{0} \\ $$$${p}+{q}=−\mathrm{1}\pm\mathrm{7}\sqrt{\mathrm{2}}\:\:=\:{c} \\ $$$${p},\:{q}\:\:{are}\:{roots}\:{of} \\ $$$${z}^{\mathrm{2}} −{cz}+\mathrm{17}=\mathrm{0} \\ $$$${z}=\frac{{c}}{\mathrm{2}}\pm\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{17}} \\ $$$${x}={p}+\mathrm{1}=\:\mathrm{1}+\frac{{c}}{\mathrm{2}}\pm\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{17}} \\ $$$${y}={q}+\mathrm{1}\:=\:\mathrm{1}+\frac{{c}}{\mathrm{2}}\mp\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{17}} \\ $$$$\:\:\:{c}\:=\:−\mathrm{1}\pm\mathrm{7}\sqrt{\mathrm{2}}\:\:\:. \\ $$
Commented by mind is power last updated on 11/Nov/19
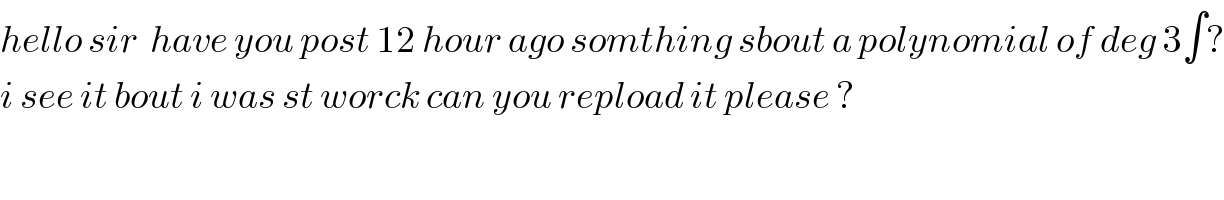
$${hello}\:{sir}\:\:{have}\:{you}\:{post}\:\mathrm{12}\:{hour}\:{ago}\:{somthing}\:{sbout}\:{a}\:{polynomial}\:{of}\:{deg}\:\mathrm{3}\int? \\ $$$${i}\:{see}\:{it}\:{bout}\:{i}\:{was}\:{st}\:{worck}\:{can}\:{you}\:{repload}\:{it}\:{please}\:? \\ $$$$ \\ $$
Commented by ajfour last updated on 12/Nov/19

$${it}\:{wasn}'{t}\:{a}\:{standard}\:{question}, \\ $$$${i}\:{shall}\:{upload}\:{another}\:{better}\:{one} \\ $$$${and}\:{request}\:{you}\:{to}\:{solve}.. \\ $$
Answered by MJS last updated on 11/Nov/19
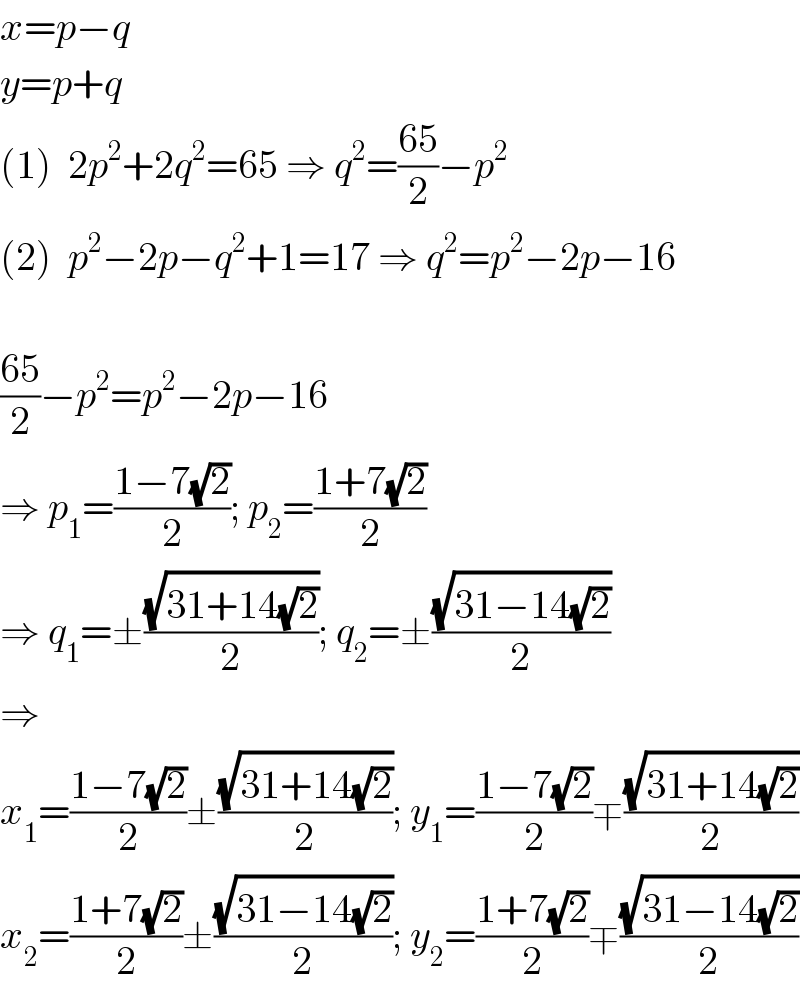
$${x}={p}−{q} \\ $$$${y}={p}+{q} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{2}{p}^{\mathrm{2}} +\mathrm{2}{q}^{\mathrm{2}} =\mathrm{65}\:\Rightarrow\:{q}^{\mathrm{2}} =\frac{\mathrm{65}}{\mathrm{2}}−{p}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:{p}^{\mathrm{2}} −\mathrm{2}{p}−{q}^{\mathrm{2}} +\mathrm{1}=\mathrm{17}\:\Rightarrow\:{q}^{\mathrm{2}} ={p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{16} \\ $$$$ \\ $$$$\frac{\mathrm{65}}{\mathrm{2}}−{p}^{\mathrm{2}} ={p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{16} \\ $$$$\Rightarrow\:{p}_{\mathrm{1}} =\frac{\mathrm{1}−\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}};\:{p}_{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{q}_{\mathrm{1}} =\pm\frac{\sqrt{\mathrm{31}+\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}};\:{q}_{\mathrm{2}} =\pm\frac{\sqrt{\mathrm{31}−\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}−\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{31}+\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}};\:{y}_{\mathrm{1}} =\frac{\mathrm{1}−\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}\mp\frac{\sqrt{\mathrm{31}+\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{31}−\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}};\:{y}_{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}\mp\frac{\sqrt{\mathrm{31}−\mathrm{14}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$
