Menu Close

x-2-y-3-23-x-3-y-2-32-solve-for-x-and-y-

Tinku Tara 0 Comments
Pin




Question Number 74801 by behi83417@gmail.com last updated on 30/Nov/19
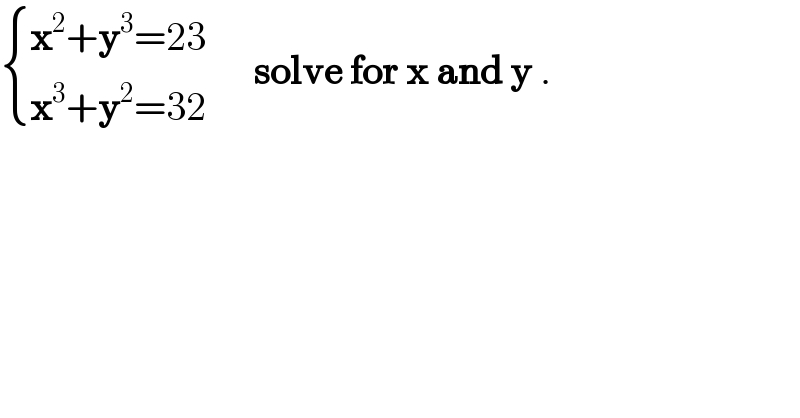
{ ((x^2 +y^3 =23)),((x^3 +y^2 =32)) :} solve for x and y .
$$\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} =\mathrm{23}}\\{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{32}}\end{cases}\:\:\:\:\:\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{y}}\:. \\ $$
Commented by MJS last updated on 30/Nov/19
if you plot these you see there′s only one real solution x≈2.96773 y≈2.42114
$$\mathrm{if}\:\mathrm{you}\:\mathrm{plot}\:\mathrm{these}\:\mathrm{you}\:\mathrm{see}\:\mathrm{there}'\mathrm{s}\:\mathrm{only}\:\mathrm{one} \\ $$$$\mathrm{real}\:\mathrm{solution} \\ $$$${x}\approx\mathrm{2}.\mathrm{96773} \\ $$$${y}\approx\mathrm{2}.\mathrm{42114} \\ $$
Commented by MJS last updated on 01/Dec/19
approximating I also found these x≈−1.88268±2.70319i; y≈−1.83861±2.44516i x≈−1.50880±3.04643i; y≈−1.29910∓2.87425i x≈−1.36613±2.49017i; y≈3.03262±.247148i x≈3.27375±.139609i; y≈−1.10548±2.02898i ...so we get 9 solutions
$$\mathrm{approximating}\:\mathrm{I}\:\mathrm{also}\:\mathrm{found}\:\mathrm{these} \\ $$$${x}\approx−\mathrm{1}.\mathrm{88268}\pm\mathrm{2}.\mathrm{70319i};\:{y}\approx−\mathrm{1}.\mathrm{83861}\pm\mathrm{2}.\mathrm{44516i} \\ $$$${x}\approx−\mathrm{1}.\mathrm{50880}\pm\mathrm{3}.\mathrm{04643i};\:{y}\approx−\mathrm{1}.\mathrm{29910}\mp\mathrm{2}.\mathrm{87425i} \\ $$$${x}\approx−\mathrm{1}.\mathrm{36613}\pm\mathrm{2}.\mathrm{49017i};\:{y}\approx\mathrm{3}.\mathrm{03262}\pm.\mathrm{247148i} \\ $$$${x}\approx\mathrm{3}.\mathrm{27375}\pm.\mathrm{139609i};\:{y}\approx−\mathrm{1}.\mathrm{10548}\pm\mathrm{2}.\mathrm{02898i} \\ $$$$…\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{9}\:\mathrm{solutions} \\ $$
Answered by behi83417@gmail.com last updated on 01/Dec/19
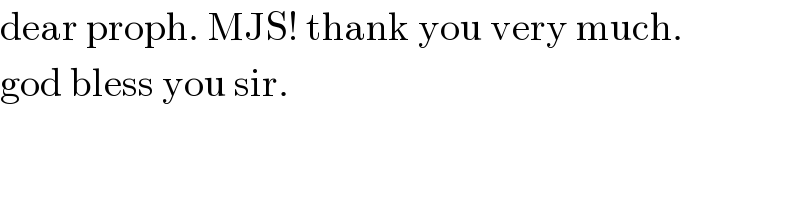
dear proph. MJS! thank you very much. god bless you sir.
$$\mathrm{dear}\:\mathrm{proph}.\:\mathrm{MJS}!\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}. \\ $$$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by ajfour last updated on 01/Dec/19
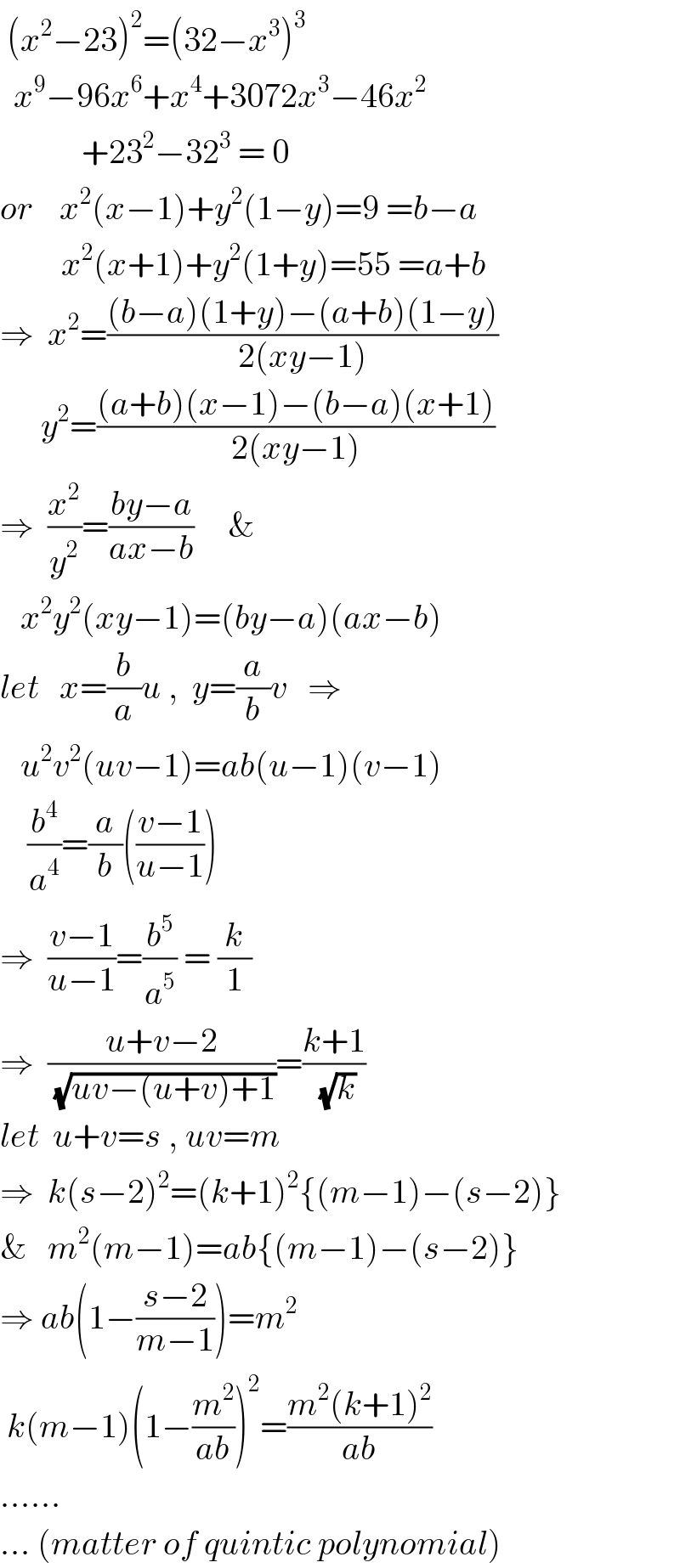
(x^2 −23)^2 =(32−x^3 )^3 x^9 −96x^6 +x^4 +3072x^3 −46x^2 +23^2 −32^3 = 0 or x^2 (x−1)+y^2 (1−y)=9 =b−a x^2 (x+1)+y^2 (1+y)=55 =a+b ⇒ x^2 =(((b−a)(1+y)−(a+b)(1−y))/(2(xy−1))) y^2 =(((a+b)(x−1)−(b−a)(x+1))/(2(xy−1))) ⇒ (x^2 /y^2 )=((by−a)/(ax−b)) & x^2 y^2 (xy−1)=(by−a)(ax−b) let x=(b/a)u , y=(a/b)v ⇒ u^2 v^2 (uv−1)=ab(u−1)(v−1) (b^4 /a^4 )=(a/b)(((v−1)/(u−1))) ⇒ ((v−1)/(u−1))=(b^5 /a^5 ) = (k/1) ⇒ ((u+v−2)/( (√(uv−(u+v)+1))))=((k+1)/( (√k))) let u+v=s , uv=m ⇒ k(s−2)^2 =(k+1)^2 {(m−1)−(s−2)} & m^2 (m−1)=ab{(m−1)−(s−2)} ⇒ ab(1−((s−2)/(m−1)))=m^2 k(m−1)(1−(m^2 /(ab)))^2 =((m^2 (k+1)^2 )/(ab)) ...... ... (matter of quintic polynomial)
$$\:\left({x}^{\mathrm{2}} −\mathrm{23}\right)^{\mathrm{2}} =\left(\mathrm{32}−{x}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$$\:\:{x}^{\mathrm{9}} −\mathrm{96}{x}^{\mathrm{6}} +{x}^{\mathrm{4}} +\mathrm{3072}{x}^{\mathrm{3}} −\mathrm{46}{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{23}^{\mathrm{2}} −\mathrm{32}^{\mathrm{3}} \:=\:\mathrm{0} \\ $$$${or}\:\:\:\:{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)+{y}^{\mathrm{2}} \left(\mathrm{1}−{y}\right)=\mathrm{9}\:={b}−{a} \\ $$$$\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+{y}^{\mathrm{2}} \left(\mathrm{1}+{y}\right)=\mathrm{55}\:={a}+{b} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} =\frac{\left({b}−{a}\right)\left(\mathrm{1}+{y}\right)−\left({a}+{b}\right)\left(\mathrm{1}−{y}\right)}{\mathrm{2}\left({xy}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:{y}^{\mathrm{2}} =\frac{\left({a}+{b}\right)\left({x}−\mathrm{1}\right)−\left({b}−{a}\right)\left({x}+\mathrm{1}\right)}{\mathrm{2}\left({xy}−\mathrm{1}\right)} \\ $$$$\Rightarrow\:\:\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }=\frac{{by}−{a}}{{ax}−{b}}\:\:\:\:\:\& \\ $$$$\:\:\:{x}^{\mathrm{2}} {y}^{\mathrm{2}} \left({xy}−\mathrm{1}\right)=\left({by}−{a}\right)\left({ax}−{b}\right) \\ $$$${let}\:\:\:{x}=\frac{{b}}{{a}}{u}\:,\:\:{y}=\frac{{a}}{{b}}{v}\:\:\:\Rightarrow \\ $$$$\:\:\:{u}^{\mathrm{2}} {v}^{\mathrm{2}} \left({uv}−\mathrm{1}\right)={ab}\left({u}−\mathrm{1}\right)\left({v}−\mathrm{1}\right) \\ $$$$\:\:\:\:\frac{{b}^{\mathrm{4}} }{{a}^{\mathrm{4}} }=\frac{{a}}{{b}}\left(\frac{{v}−\mathrm{1}}{{u}−\mathrm{1}}\right) \\ $$$$\Rightarrow\:\:\frac{{v}−\mathrm{1}}{{u}−\mathrm{1}}=\frac{{b}^{\mathrm{5}} }{{a}^{\mathrm{5}} }\:=\:\frac{{k}}{\mathrm{1}} \\ $$$$\Rightarrow\:\:\frac{{u}+{v}−\mathrm{2}}{\:\sqrt{{uv}−\left({u}+{v}\right)+\mathrm{1}}}=\frac{{k}+\mathrm{1}}{\:\sqrt{{k}}} \\ $$$${let}\:\:{u}+{v}={s}\:,\:{uv}={m} \\ $$$$\Rightarrow\:\:{k}\left({s}−\mathrm{2}\right)^{\mathrm{2}} =\left({k}+\mathrm{1}\right)^{\mathrm{2}} \left\{\left({m}−\mathrm{1}\right)−\left({s}−\mathrm{2}\right)\right\} \\ $$$$\&\:\:\:{m}^{\mathrm{2}} \left({m}−\mathrm{1}\right)={ab}\left\{\left({m}−\mathrm{1}\right)−\left({s}−\mathrm{2}\right)\right\} \\ $$$$\Rightarrow\:{ab}\left(\mathrm{1}−\frac{{s}−\mathrm{2}}{{m}−\mathrm{1}}\right)={m}^{\mathrm{2}} \\ $$$$\:{k}\left({m}−\mathrm{1}\right)\left(\mathrm{1}−\frac{{m}^{\mathrm{2}} }{{ab}}\right)^{\mathrm{2}} =\frac{{m}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} }{{ab}} \\ $$$$…… \\ $$$$…\:\left({matter}\:{of}\:{quintic}\:{polynomial}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *