Menu Close

x-2-y-x-2-1-3-2-1-

Tinku Tara
Pin




Question Number 204 by 02@>@0 last updated on 25/Jan/15
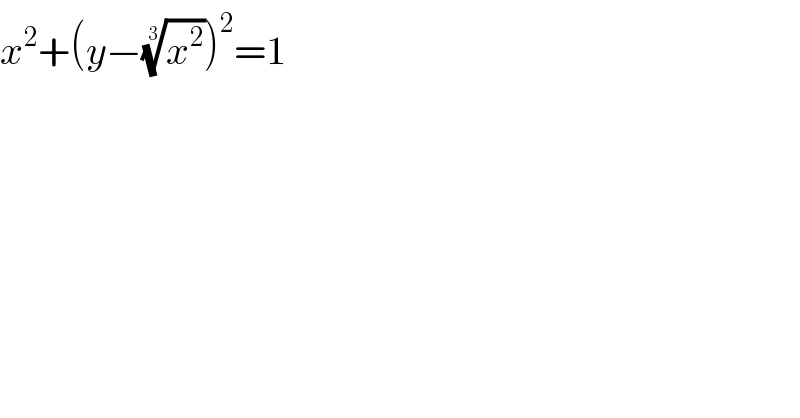
x^2 +(y−(x^2 )^(1/3) )^2 =1
$${x}^{\mathrm{2}} +\left({y}−\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{1} \\ $$
Commented by 02@>@0 last updated on 15/Dec/14
$$ \\ $$
Answered by 02@>@0 last updated on 15/Dec/14
$$ \\ $$
Answered by 02@>@0 last updated on 15/Dec/14
$$ \\ $$
Answered by prakash jain last updated on 16/Dec/14
put x^2 =u^3 u^3 +(y−u)^2 =1 u^3 +y^2 −2uy+u^2 =1 y^2 −2uy+(u^3 +u^2 −1)=0 y=((2u±(√(4u^2 −4(u^3 +u^2 −1))))/2) y=((2u±(√(4−4u^3 )))/2)=(x^2 )^(1/3) ±(√(1−x^2 ))
$$\mathrm{put}\:{x}^{\mathrm{2}} ={u}^{\mathrm{3}} \\ $$$${u}^{\mathrm{3}} +\left({y}−{u}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${u}^{\mathrm{3}} +{y}^{\mathrm{2}} −\mathrm{2}{uy}+{u}^{\mathrm{2}} =\mathrm{1} \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{uy}+\left({u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${y}=\frac{\mathrm{2}{u}\pm\sqrt{\mathrm{4}{u}^{\mathrm{2}} −\mathrm{4}\left({u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{2}{u}\pm\sqrt{\mathrm{4}−\mathrm{4}{u}^{\mathrm{3}} }}{\mathrm{2}}=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }\pm\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$
Commented by prakash jain last updated on 16/Dec/14
To get x in terms of y solve the cubic equation u^3 +u^2 −2uy+(y^2 −1)=0
$$\mathrm{To}\:\mathrm{get}\:{x}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{y}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{cubic}\:\mathrm{equation} \\ $$$${u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{2}{uy}+\left({y}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$

Pin