Question Number 141749 by Huy last updated on 23/May/21
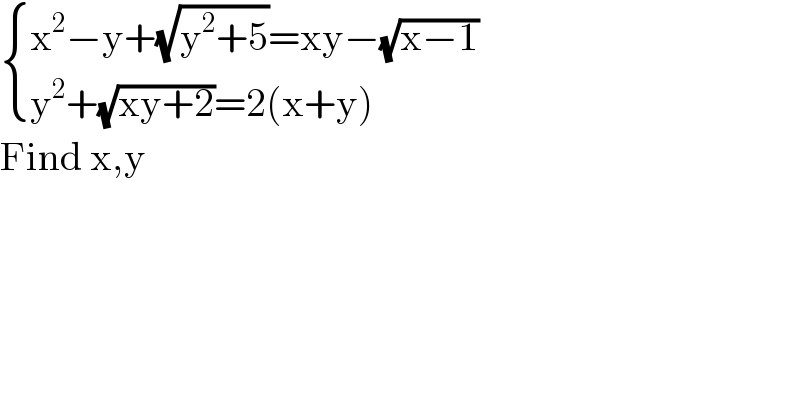
$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{y}+\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{5}}=\mathrm{xy}−\sqrt{\mathrm{x}−\mathrm{1}}}\\{\mathrm{y}^{\mathrm{2}} +\sqrt{\mathrm{xy}+\mathrm{2}}=\mathrm{2}\left(\mathrm{x}+\mathrm{y}\right)}\end{cases} \\ $$$$\mathrm{Find}\:\mathrm{x},\mathrm{y} \\ $$
Answered by MJS_new last updated on 23/May/21
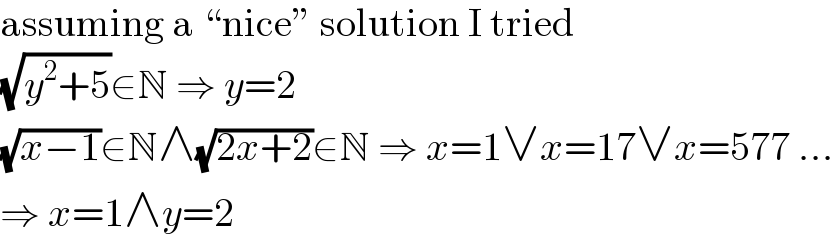
$$\mathrm{assuming}\:\mathrm{a}\:“\mathrm{nice}''\:\mathrm{solution}\:\mathrm{I}\:\mathrm{tried} \\ $$$$\sqrt{{y}^{\mathrm{2}} +\mathrm{5}}\in\mathbb{N}\:\Rightarrow\:{y}=\mathrm{2} \\ $$$$\sqrt{{x}−\mathrm{1}}\in\mathbb{N}\wedge\sqrt{\mathrm{2}{x}+\mathrm{2}}\in\mathbb{N}\:\Rightarrow\:{x}=\mathrm{1}\vee{x}=\mathrm{17}\vee{x}=\mathrm{577}\:… \\ $$$$\Rightarrow\:{x}=\mathrm{1}\wedge{y}=\mathrm{2} \\ $$
