x-2-yz-1-y-2-xz-2-z-2-xy-3-x-y-z-

Question Number 74912 by behi83417@gmail.com last updated on 03/Dec/19

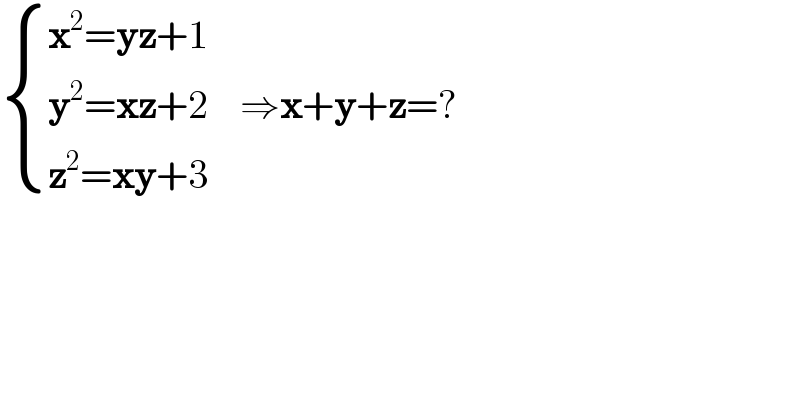
$$\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\boldsymbol{\mathrm{yz}}+\mathrm{1}}\\{\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\boldsymbol{\mathrm{xz}}+\mathrm{2}}\\{\boldsymbol{\mathrm{z}}^{\mathrm{2}} =\boldsymbol{\mathrm{xy}}+\mathrm{3}}\end{cases}\:\:\:\:\Rightarrow\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{z}}=? \\ $$

Answered by MJS last updated on 03/Dec/19

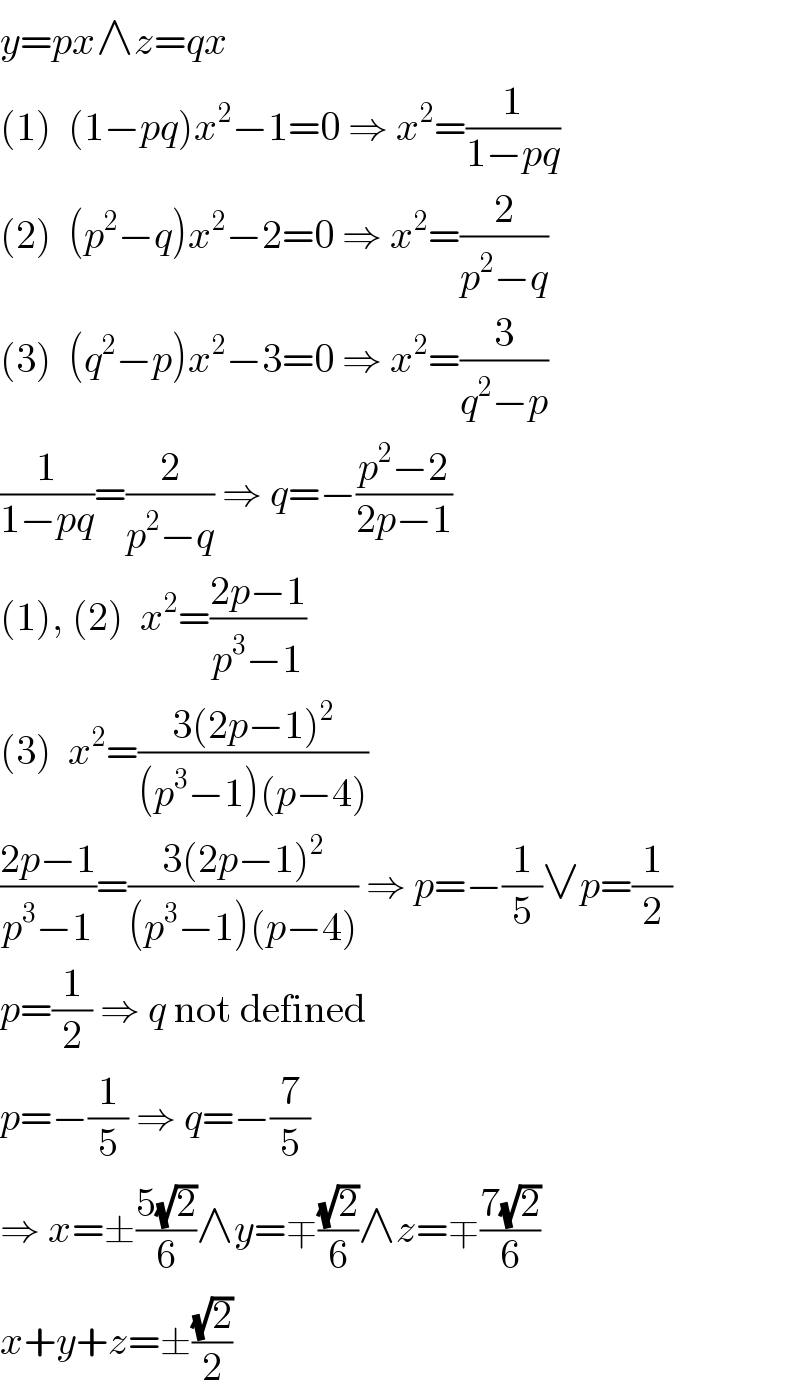
y=px∧z=qx (1) (1−pq)x^2 −1=0 ⇒ x^2 =(1/(1−pq)) (2) (p^2 −q)x^2 −2=0 ⇒ x^2 =(2/(p^2 −q)) (3) (q^2 −p)x^2 −3=0 ⇒ x^2 =(3/(q^2 −p)) (1/(1−pq))=(2/(p^2 −q)) ⇒ q=−((p^2 −2)/(2p−1)) (1), (2) x^2 =((2p−1)/(p^3 −1)) (3) x^2 =((3(2p−1)^2 )/((p^3 −1)(p−4))) ((2p−1)/(p^3 −1))=((3(2p−1)^2 )/((p^3 −1)(p−4))) ⇒ p=−(1/5)∨p=(1/2) p=(1/2) ⇒ q not defined p=−(1/5) ⇒ q=−(7/5) ⇒ x=±((5(√2))/6)∧y=∓((√2)/6)∧z=∓((7(√2))/6) x+y+z=±((√2)/2)

$${y}={px}\wedge{z}={qx} \\ $$$$\left(\mathrm{1}\right)\:\:\left(\mathrm{1}−{pq}\right){x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}−{pq}} \\ $$$$\left(\mathrm{2}\right)\:\:\left({p}^{\mathrm{2}} −{q}\right){x}^{\mathrm{2}} −\mathrm{2}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{2}}{{p}^{\mathrm{2}} −{q}} \\ $$$$\left(\mathrm{3}\right)\:\:\left({q}^{\mathrm{2}} −{p}\right){x}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{3}}{{q}^{\mathrm{2}} −{p}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{pq}}=\frac{\mathrm{2}}{{p}^{\mathrm{2}} −{q}}\:\Rightarrow\:{q}=−\frac{{p}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{p}−\mathrm{1}} \\ $$$$\left(\mathrm{1}\right),\:\left(\mathrm{2}\right)\:\:{x}^{\mathrm{2}} =\frac{\mathrm{2}{p}−\mathrm{1}}{{p}^{\mathrm{3}} −\mathrm{1}} \\ $$$$\left(\mathrm{3}\right)\:\:{x}^{\mathrm{2}} =\frac{\mathrm{3}\left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{2}} }{\left({p}^{\mathrm{3}} −\mathrm{1}\right)\left({p}−\mathrm{4}\right)} \\ $$$$\frac{\mathrm{2}{p}−\mathrm{1}}{{p}^{\mathrm{3}} −\mathrm{1}}=\frac{\mathrm{3}\left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{2}} }{\left({p}^{\mathrm{3}} −\mathrm{1}\right)\left({p}−\mathrm{4}\right)}\:\Rightarrow\:{p}=−\frac{\mathrm{1}}{\mathrm{5}}\vee{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{q}\:\mathrm{not}\:\mathrm{defined} \\ $$$${p}=−\frac{\mathrm{1}}{\mathrm{5}}\:\Rightarrow\:{q}=−\frac{\mathrm{7}}{\mathrm{5}} \\ $$$$\Rightarrow\:{x}=\pm\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{6}}\wedge{y}=\mp\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\wedge{z}=\mp\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$${x}+{y}+{z}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$

Commented by behi83417@gmail.com last updated on 04/Dec/19

dear proph : MJS! it is great.thank you very much sir.

$$\mathrm{dear}\:\mathrm{proph}\::\:\mathrm{MJS}!\:\mathrm{it}\:\mathrm{is}\:\mathrm{great}.\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

x-2-yz-1-y-2-xz-2-z-2-xy-3-x-y-z-

Leave a Reply Cancel reply