Menu Close

x-2-yz-3-y-2-zx-5-z-2-xy-1-solve-for-x-y-and-z-

Tinku Tara 0 Comments
Pin




Question Number 135191 by liberty last updated on 11/Mar/21
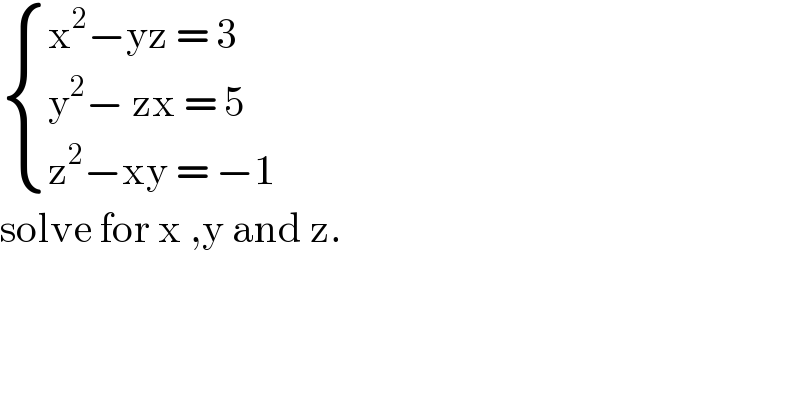
{ ((x^2 −yz = 3)),((y^2 − zx = 5)),((z^2 −xy = −1)) :} solve for x ,y and z.
$$\begin{cases}{\mathrm{x}^{\mathrm{2}} −\mathrm{yz}\:=\:\mathrm{3}}\\{\mathrm{y}^{\mathrm{2}} −\:\mathrm{zx}\:=\:\mathrm{5}}\\{\mathrm{z}^{\mathrm{2}} −\mathrm{xy}\:=\:−\mathrm{1}}\end{cases} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\:,\mathrm{y}\:\mathrm{and}\:\mathrm{z}. \\ $$
Answered by MJS_new last updated on 11/Mar/21
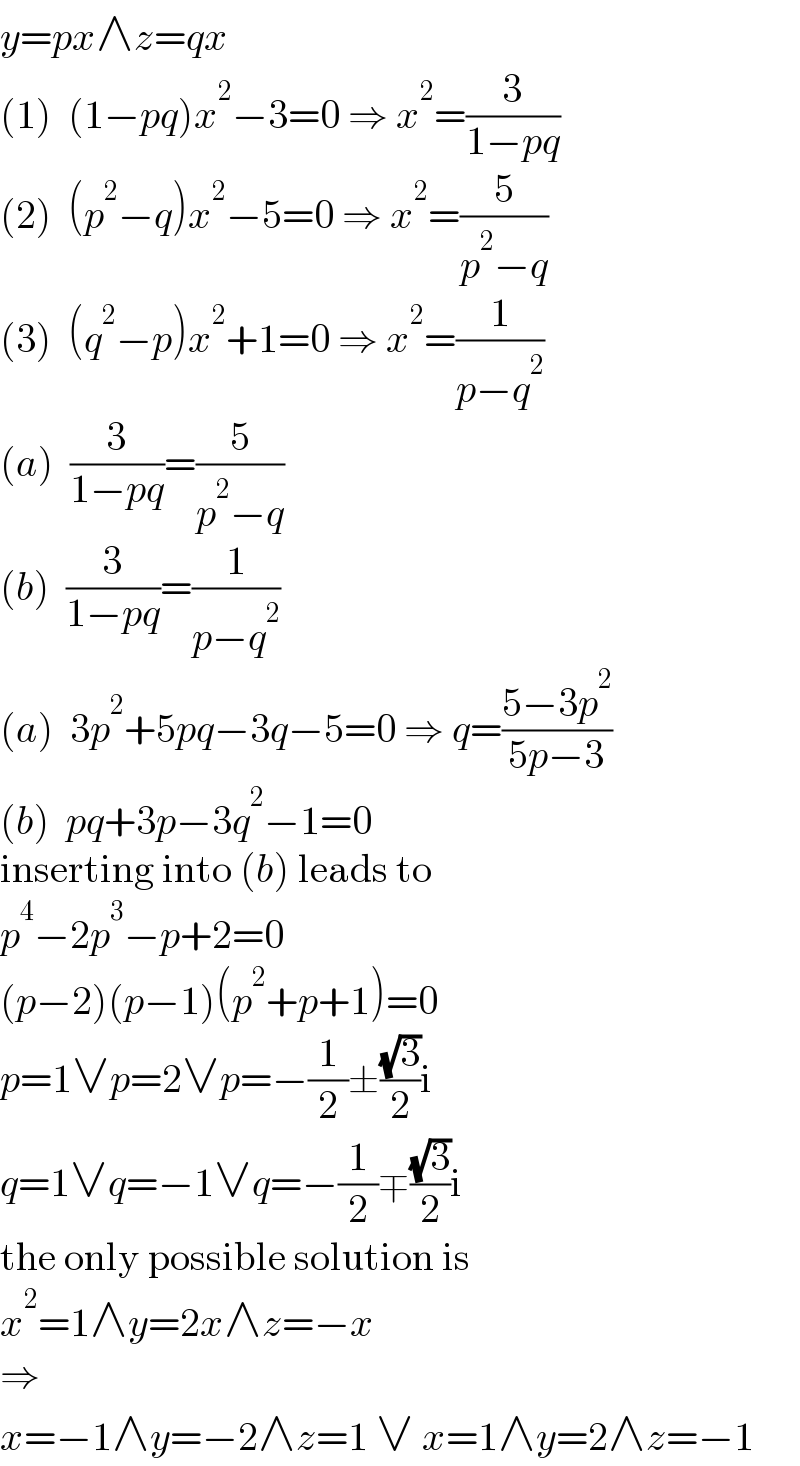
y=px∧z=qx (1) (1−pq)x^2 −3=0 ⇒ x^2 =(3/(1−pq)) (2) (p^2 −q)x^2 −5=0 ⇒ x^2 =(5/(p^2 −q)) (3) (q^2 −p)x^2 +1=0 ⇒ x^2 =(1/(p−q^2 )) (a) (3/(1−pq))=(5/(p^2 −q)) (b) (3/(1−pq))=(1/(p−q^2 )) (a) 3p^2 +5pq−3q−5=0 ⇒ q=((5−3p^2 )/(5p−3)) (b) pq+3p−3q^2 −1=0 inserting into (b) leads to p^4 −2p^3 −p+2=0 (p−2)(p−1)(p^2 +p+1)=0 p=1∨p=2∨p=−(1/2)±((√3)/2)i q=1∨q=−1∨q=−(1/2)∓((√3)/2)i the only possible solution is x^2 =1∧y=2x∧z=−x ⇒ x=−1∧y=−2∧z=1 ∨ x=1∧y=2∧z=−1
$${y}={px}\wedge{z}={qx} \\ $$$$\left(\mathrm{1}\right)\:\:\left(\mathrm{1}−{pq}\right){x}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{1}−{pq}} \\ $$$$\left(\mathrm{2}\right)\:\:\left({p}^{\mathrm{2}} −{q}\right){x}^{\mathrm{2}} −\mathrm{5}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{5}}{{p}^{\mathrm{2}} −{q}} \\ $$$$\left(\mathrm{3}\right)\:\:\left({q}^{\mathrm{2}} −{p}\right){x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{{p}−{q}^{\mathrm{2}} } \\ $$$$\left({a}\right)\:\:\frac{\mathrm{3}}{\mathrm{1}−{pq}}=\frac{\mathrm{5}}{{p}^{\mathrm{2}} −{q}} \\ $$$$\left({b}\right)\:\:\frac{\mathrm{3}}{\mathrm{1}−{pq}}=\frac{\mathrm{1}}{{p}−{q}^{\mathrm{2}} } \\ $$$$\left({a}\right)\:\:\mathrm{3}{p}^{\mathrm{2}} +\mathrm{5}{pq}−\mathrm{3}{q}−\mathrm{5}=\mathrm{0}\:\Rightarrow\:{q}=\frac{\mathrm{5}−\mathrm{3}{p}^{\mathrm{2}} }{\mathrm{5}{p}−\mathrm{3}} \\ $$$$\left({b}\right)\:\:{pq}+\mathrm{3}{p}−\mathrm{3}{q}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{inserting}\:\mathrm{into}\:\left({b}\right)\:\mathrm{leads}\:\mathrm{to} \\ $$$${p}^{\mathrm{4}} −\mathrm{2}{p}^{\mathrm{3}} −{p}+\mathrm{2}=\mathrm{0} \\ $$$$\left({p}−\mathrm{2}\right)\left({p}−\mathrm{1}\right)\left({p}^{\mathrm{2}} +{p}+\mathrm{1}\right)=\mathrm{0} \\ $$$${p}=\mathrm{1}\vee{p}=\mathrm{2}\vee{p}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$${q}=\mathrm{1}\vee{q}=−\mathrm{1}\vee{q}=−\frac{\mathrm{1}}{\mathrm{2}}\mp\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{is} \\ $$$${x}^{\mathrm{2}} =\mathrm{1}\wedge{y}=\mathrm{2}{x}\wedge{z}=−{x} \\ $$$$\Rightarrow \\ $$$${x}=−\mathrm{1}\wedge{y}=−\mathrm{2}\wedge{z}=\mathrm{1}\:\vee\:{x}=\mathrm{1}\wedge{y}=\mathrm{2}\wedge{z}=−\mathrm{1} \\ $$
Answered by benjo_mathlover last updated on 11/Mar/21
adding the three equation gives ⇒x^2 +y^2 +z^2 −(xy+xz+yz)=7 ⇒2(x^2 +y^2 +z^2 )−2(xy+xz+yz)=14 let u=x−y , v=y−z and w=z−x we get u^2 +v^2 +w^2 = 14 while obviously u+v+w = 0 w = −(u+v) substituing gives u^2 +v^2 +uv = 7 .now substract the equation y^2 −zx=5 from first one in the original problem x^2 −y^2 +zx−zy = −2 (x−y)(x+y+z)=−2...(i) ⇒the third from the second gives (y−z)(x+y+z)=6 ...(2) (u,v)=(x−y,y−z) we see that v=−3u and u^2 =1 so (u,v)=(1,−3)or (−1,3) . case(1) { ((x=y+1)),((z=y+3)) :} substituting the equation y^2 =5+zx we find the solution { (((−1,−2,1) and)),(((1,2,−1))) :}
$$\mathrm{adding}\:\mathrm{the}\:\mathrm{three}\:\mathrm{equation}\:\mathrm{gives} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} −\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)=\mathrm{7} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right)−\mathrm{2}\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)=\mathrm{14} \\ $$$$\mathrm{let}\:\mathrm{u}=\mathrm{x}−\mathrm{y}\:,\:\mathrm{v}=\mathrm{y}−\mathrm{z}\:\mathrm{and}\:\mathrm{w}=\mathrm{z}−\mathrm{x} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} +\mathrm{w}^{\mathrm{2}} \:=\:\mathrm{14}\: \\ $$$$\mathrm{while}\:\mathrm{obviously}\:\mathrm{u}+\mathrm{v}+\mathrm{w}\:=\:\mathrm{0} \\ $$$$\mathrm{w}\:=\:−\left(\mathrm{u}+\mathrm{v}\right)\:\mathrm{substituing}\:\mathrm{gives} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} +\mathrm{uv}\:=\:\mathrm{7}\:.\mathrm{now}\:\mathrm{substract}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{y}^{\mathrm{2}} −\mathrm{zx}=\mathrm{5}\:\mathrm{from}\:\mathrm{first}\:\mathrm{one} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{original}\:\mathrm{problem}\: \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{zx}−\mathrm{zy}\:=\:−\mathrm{2} \\ $$$$\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=−\mathrm{2}…\left(\mathrm{i}\right) \\ $$$$\Rightarrow\mathrm{the}\:\mathrm{third}\:\mathrm{from}\:\mathrm{the}\:\mathrm{second}\:\mathrm{gives} \\ $$$$\left(\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)=\mathrm{6}\:…\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{x}−\mathrm{y},\mathrm{y}−\mathrm{z}\right)\:\mathrm{we}\:\mathrm{see}\:\mathrm{that}\: \\ $$$$\mathrm{v}=−\mathrm{3u}\:\mathrm{and}\:\mathrm{u}^{\mathrm{2}} =\mathrm{1}\:\mathrm{so}\:\left(\mathrm{u},\mathrm{v}\right)=\left(\mathrm{1},−\mathrm{3}\right)\mathrm{or} \\ $$$$\left(−\mathrm{1},\mathrm{3}\right)\:.\:\mathrm{case}\left(\mathrm{1}\right)\:\begin{cases}{\mathrm{x}=\mathrm{y}+\mathrm{1}}\\{\mathrm{z}=\mathrm{y}+\mathrm{3}}\end{cases} \\ $$$$\mathrm{substituting}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\mathrm{y}^{\mathrm{2}} =\mathrm{5}+\mathrm{zx}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\: \\ $$$$\begin{cases}{\left(−\mathrm{1},−\mathrm{2},\mathrm{1}\right)\:\mathrm{and}}\\{\left(\mathrm{1},\mathrm{2},−\mathrm{1}\right)}\end{cases} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *